Question: Let X be a continuous variable for which the expectation E(X) exists. Show that the following holds: (Hint: Making use of Proposition 6.7 for the

Let X be a continuous variable for which the expectation E(X) exists. Show that the following holds: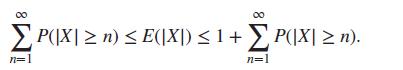P(|X| n) E(|X|) 1+ P(|X| n). n=1 n=1

(Hint: Making use of Proposition 6.7 for the nonnegative variable Y = |X|, express the expected value of Y as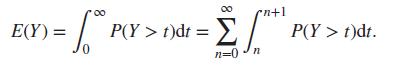image text in transcribed

Then observe that for t ∈ [n, n + 1), we have P(Y ≥ n + 1) ≤ P(Y > t) ≤ P(Y ≥ n).)

P(|X| n) E(|X|) 1+ P(|X| n). n=1 n=1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

Q:

lup ] (d) Show how a generating (or "mother") wavelet (x) can spawn a family of "daughter" wavelets jk(x) by simple shifting and scaling operations, and explain the advantages of representing...

Q:

For each statement below, say whether it's true or false; if true without further assumptions, briefly explain why it's true (and ? extra credit ? what its implications are for statistical...

Q:

Set Student Name: 1. Describe the relationship between two variables that have a correlation coefficient value: a. Near -1 b. Near 0 c. Near 1 2. Data was collected where a weightlifter was asked to...

Q:

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

Q:

Consider the Markov Chain, Xn, on the states i = 0, 1, 2, . . . with transition matrix given by pi,i1 = p i = 1, 2, . . . pi,i+1 = 1 p i = 0, 1, . . . p0,0 = p where 0

Q:

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

Q:

When developing financial statement forecasts, analysts should most likely: a) Develop possibilities relying exclusively on the results of financial analysis b) Use the results of financial analysis,...

Q:

(1) Let f : [n] r [n] be a permutation. Axed point of f is an element x E [n] such that f(x) = x. Now consider random permutations of [n] and let X be the random variable which represents the number...

Q:

Extending the variance of the sum rule. For mathematical convenience we first extend the sum rule to three random variables with zero expectation. Next we further extend the rule to three random...

Q:

Create charts to better understand data sets. For cross-sectional data, use a scatter chart. For time series data, use a line chart. Linear y = a + bx Logarithmic y = ln(x) Polynomial (2nd order) y =...

Q:

Phil Eubanks engaged in the following activities in establishing his photography studio, Picture This!: 1. Opened a bank account in the name of Picture This! and deposited $8,000 of his own money...

Q:

Consider a city center where the traffic conditions are described by a Macroscopic Fundamental Diagram (MFD) of network outflow (g- rate of trips finished) vs. accumulation (n- number of cars) with a...

Q:

17. Consumption is equal to 5,000 at a disposable income of . ( LO5 ) a) $2,000 billion d) $8,000 billion b) $4,000 billion e) $10,000 billion c) $6,000 billion

Q:

What is the definition of cooperative strategy, and why is this strategy important to firms competing in the current competitive landscape?

Q:

Suppose that a machine's operation is regarded as a system having three main components: \(A\) (team), \(B\) (power supply), and \(C\) (assembly). Suppose, furthermore, that component \(\mathrm{A}\)...

Q:

A system consists of 6 components connected as in Figure 16.3. Find the overall reliability of the system, given that the reliabilities of \(A, B, C, D, E\), and \(F\) are, respectively,...

Q:

A system consists of 5 identical components connected in parallel. Determine the reliability of each component if the overall reliability of the system is to be 0.96 ?

Q:

Assuming the nominal interest rate (APR) of 8%, what is the effective annual rate (EAR) when the interest rate compounds semiannually? O 8.18% O 8.16% O 8.12% O 8.09%

Q:

6. (2 points) Tom enters into a like-kind exchange is which he will transfer land with a FMV of $80,000 and an A/B of $52,000 to his exchange partner. Tom will receive land worth $68,000 and the...

Q:

Effect of Dout Accounts in Net Income During its first year of operations, Mack's Pumbing Supply Co. had sales of $520,000, wrote off $8,000 of accounts as uncollectible using the direct write-off...