Let X be a random variable having the binomial distribution with parameters n and p.

(i) Show that its probability function f (x), x = 0, 1,…, n, can be calculated via the recursive relation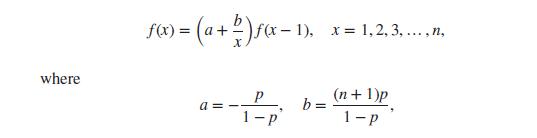

with initial condition f (0) = (1 − p)n.
(ii) Show that f (x) > f (x − 1) if and only if x (iii) Verify that, if the product (n + 1)p is not an integer, f attains its maximum at the point x0 = [(n + 1)p]. What happens if (n + 1)p is an integer?
Application: A footballer, who likes to take penalty kicks, has an 80% probability of scoring in each penalty. If he shoots 10 penalty kicks for his team during a football season, for what value of k is the probability that he scores k goals in these 10 attempts maximized? For this value of k, what is the probability that he scores k goals in 10 penalty kicks?

where f(x) = c) = (a + b) f(x 1), 1), x=1, 2, 3,...,n, P a= b = (n+1)p 1-P 1-p