Let X be a random variable with a b(n, p) distribution. Show that for any positive integer r, the rth factorial moment of X

????(r) = E[(X)r] = E[X(X − 1)(X − 2) · · · (X − r + 1)]

is given by the formula

????(r) = (n)rpr = n(n − 1)(n − 2) · · · (n − r + 1)pr, 1 ≤ r ≤ n.

In particular, for r = 1, 2, verify that we get the same results as those derived in Proposition 5.2.

(

Hint: You may find it useful to use the identity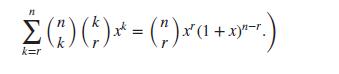

n (*) (*)** = (7)x+x) n k=r