Question: Let X be a random variable with density function which is the density of the Cauchy distribution see Exercise 12 of Section 6.2. Prove

Let X be a random variable with density function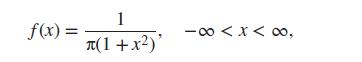1 f(x) = (1+x)' -8

which is the density of the Cauchy distribution – see Exercise 12 of Section 6.2.
Prove that the expectation of X does not exist.

1 f(x) = (1+x)' -8

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

Q:

Set Student Name: 1. Describe the relationship between two variables that have a correlation coefficient value: a. Near -1 b. Near 0 c. Near 1 2. Data was collected where a weightlifter was asked to...

Q:

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

Q:

Consider the following situation. Suppose we have two fair dice, D1 with 5 red sides and 1 white side and D2 with 1 red side and 5 white sides. We pick one of the dice randomly, and throw it...

Q:

Economics 257 November 9, 2016 R. Davidson Assignment 3 1. This exercise is closely related to one on the previous assignment. Let p denote the proportion of individuals in a population that suer...

Q:

GIVE DETAILED WORKING IN ALL QUESTIONS. Suppose that a game is to be played with a single die assumed fair. In this game a player wins $20 if a 2 turns up, $40 if a 4 turns up; loses $30 if a 6 turns...

Q:

Hello I need help with this part of the assignment , please , thank you Problem(14) (10 points) Consider a random experiment of throwing two fair dice together. Define the following events: A: { You...

Q:

The best definition for nonparametric statistics I can think of is when data does not fit inside the normal parameters of a normal distribution, it calls for the use of this statistical method....

Q:

2.38. A coin is tossed three times. If X is a random variable giving the number of heads that arise, construct a table showing the probability distribution of X. 2.39. An urn holds 5 white and 3...

Q:

Show the workings in each. 20. Compare the adjustment to medium run equilibrium after a fiscal contraction of a fixed and flexible exchange rate economy. What happens in the short run and during the...

Q:

Problem 1 (a) Let Y be a random variable with the following distribution f (y): ----n y) 0.1 0.2 0.1 0.6 compute the standard deviation of Y. (b) The proportion of people who respond to a certain...

Q:

Assume a standard Normal distribution. Draw a separate, well-labelled Normal curve for each part. a. Find an approximate z-score that gives a left area of 0.7000. b. Find an approximate z-score that...

Q:

The company purchased the following securities during Year 1: In Year 2, the company reclassified both of these securities. Security A was reclassified as held to maturity; the fair value of security...

Q:

f p varies directly as r ^ ( 2 ) and p = 3 2 when r = 4 find the value of p when r = 6 . 5

Q:

What is the definition of cooperative strategy, and why is this strategy important to firms competing in the current competitive landscape?

Q:

The following are the self-reported times (hours for month), spent on homework, by random samples of juniors in two different majors. Use the \(U\) test at the 0.05 level of significance to test...

Q:

Comparing two types of automobile engines, a consumer testing service obtained the following pickup ( \(0-100 \mathrm{kmph})\) times (rounded to the nearest tenth of a second): Use the \(U\) test at...

Q:

The following are the number of classes attended by 2 students on 20 days: 3 and 5, 1 and 2, 3 and 4, 2 and 5, 5 and 3, 4 and 2, 1 and 3, 1 and 4, 1 and 2, 2 and 4, 3 and 2, 2 and 5, 5 and 5,1 and...

Q:

Which of the following is not one of the measures discussed in lecture to assess the financial risk of retailers? cash flow analysis O quick ratio debt ratio current ratio

Q:

At December 31, 2020, Smiley Corp. had 200,000 shares of common stock and 12,000 shares of 6%, $100 par value cumulative preferred stock outstanding. No dividends were declared during 2020. Net...

Q:

The following information relates to Blossom, Inc.: For the Year Ended December 31, 2020 2021 Plan assets (at fair value) $1416000 $2086000 Pension expense 725000 558000 Projected benefit obligation...