Question: Let X be a random variable with EX = 0 and Var(X) = 2 . We would like to prove that for any a

Let X be a random variable with EX = 0 and Var(X) = σ². We would like to prove that for any a > 0, we have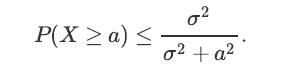 P(X a) 0 + a

This inequality is sometimes called the one-sided Chebyshev inequality. One way to show this is to use P(X ≥ a) = P(X + c ≥ a + c) for any constant c ∈ R.

P(X a) 0 + a

Step by Step Solution

★★★★★

3.42 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To prove the onesided Chebyshev inequality we can use the following technique Given X is a random va... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

The number of customers visiting a store during a day is a random variable with mean EX = 100 and variance Var(X) = 225. 1. Using Chebyshev's inequality, find an upper bound for having more than 120...

Beginning inventory, purchases, and sales for Item Zeta9 are as follows: Oct. 1 Inventory 45 units @$24 7 Sale. 32 units 15 Purchase 31 units @ $28 24 Sale 19 units Assuming a perpetual inventory...

Let X be a random variable with moment-generating function Mx(t), -h )

Please solve (i) and (ii)(b) only Al. (i) Let X be a random variable with E[|X]] 0. Prove the Chebyshev inequality: for any & > 0, P ( IX | ZE )S E[IX | ~ ] Ea [5 marks] (ii) Let Xn, n 2 1, be a...

=+17. Let X be a random variable with E(X) = 0 and E(X2) = 2. Show that Pr(X c) a2 + 2 (a + c)2 (3.9) for all nonnegative a and c. Prove that the choice a = 2/c minimizes the right-hand side of...

1. A portfolio manager is expected to stay within 75 basis points of a benchmark index 90 percent of the time. The manager meets this objecti ve in six out of eight quarters. Calculate the...

Let X be a random variable with EX = 1 and R X = (0, 2). If Y = X 3 6X 2 , show that EY 5.

Let X be a random variable with P(X = 0) = P(X = 1) = P(X = 2) = and P(X = 3) = /1. (a) Find the expectation of (i) X (ii) x (b) What is the variance of X?

PLEASE ANSWER ALL QUESTIONS 3.105. Let X be a random variable that can take on the values 2, 1, and 3 with respective probabilities 1 3, 1 6, and 1 2. Find (a) the mean, (b) the variance, (c) the...

(One-sided Chebyshev bound) Let X be a random variable such that E(X) = 0 and Var(X) = ????2. Show that, for any a > 0, This result is known as Cantellis inequality. (Hint: For b > 0, put W = (X +...

Why is it important for an e-business model to create value in a way that is differentiated from the way competitors models create value?

Give an example, other than those described in this chapter, of a weak entity type. Why is it necessary to indicate an identifying relationship?

4.81 Referring to the random variables whose joint probability density function is given in Exercise 3.47 on page 125, find the average amount of kerosene left in the tank at the end of the day.

We say leadership involves influencing organized groups toward goals. Do you see any disadvantages to restricting the definition to organized groups?

In how many ways can 4 out of 11 similar propellers be fitted on an airplane?

CCTV cameras are to be fitted at six fixed places in a bank. In how many ways can the six available CCTV cameras be fitted at the six places in the bank?

The quality of surround sound from four digital movie systems is to be rated superior, average, or inferior, and we are interested only in how many of the systems get each of these ratings. Draw a...

On May 7, Carpet Barn Company offered to pay $71,780 for land that had a selling price of $90,000. On May 15, Carpet Barn accepted a counteroffer of $83,090. On June 5, the land was assessed at a...

How much would $1, growing at 13.7% per year, be worth after 75 years?

Ploeger Corporation has provided the following contribution format income statement. Assume that the following information is within the relevant range. Sales (4,000 units): $240,000 Variable...