Let Y 1 , Y 2 , Y 3 , be a sequence of i i d random variables with mean EY i and finite variance Var(Y i ) 2 Define the sequence X n ,n 2, 3, as Xn YY2 Y2Y3 Yn 1Yn YY Show that X n for n 2,3,

Question: Let Y 1 , Y 2 , Y 3 , be a sequence of i.i.d. random variables with mean EY i = and

Let Y₁, Y₂, Y₃, ⋯ be a sequence of i.i.d. random variables with mean EY_i = μ and finite variance Var(Y_i) = σ². Define the sequence {X_n,n = 2, 3, . . . } as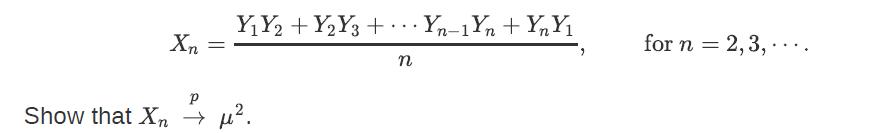 Xn = YY2 + Y2Y3+ Yn-1Yn + YY . Show that X n for n = 2,3,.

Xn = YY2 + Y2Y3+ Yn-1Yn + YY . Show that X n for n = 2,3,.

Step by Step Solution

★★★★★

3.54 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Surebased on the information you providedthe image shows the following definition for the sequence Xn Xn Y1Y2 Y2Y3 Yn1Yn YnY1 for n 2 3 HereY1Y2Y3are ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

Let Xn be a sequence of random variables that converges in distribution to a random variable X. Let Yn be a sequence of random variables with the property that for any finite number c, Show that for...

Let X (t) be a Poisson counting process with arrival rate, . We form two related counting processes, Y1 (t) and Y2 (t), by randomly splitting the Poisson process, X (t). In random splitting, the i th...

Let Xk, k = 1, 2, 3¦ be a sequence of IID random variables with finite mean, , and let Sn be the sequence of sample means, (a) Show that the characteristic function of Sn can be written as (b)...

QUESTION 5 TOTAL 19 marks 1. Suppose that X;, X;,... is a sequence of ii.d. random variables with y = EX;, where g # +oco. Let 5, = X + .-+ X,,. Define the event A= {nlim Sy exists} : (a) What is...

(c) part and Second Question (a) and (c) part only (c) Let Y, = Z, + 0 Z, , where (Z.) be a sequence of iid random variables with mean zero and variance o-. Show that a real valued function on Z,...

1 2.3 Definition of a Discrete Probability Function Definition: Let S be a discrete sample space from some experiment. A function P, defined on all events in S, is said to be a probability function...

Please explain to me clearly and show how to do the two suppositions in the (question) file. Please take a look at the (notes) file and see the material up to the questions will be needed to answer...

urgent solution for part c) and d) needed, thank you (25 pts) Central Limit Theorem. Let X1, X2, X3, be a sequence of i.i.d. random variables with finite mean u and finite variance o?, and let Zn be...

please make sure to show all steps and explain them. thanks ! Let /V be a random variable with mean E [M] = m, and Var (N) = v; let A1, A2, ... be a sequence of i.i.d random variables, all...

. In certain gambling situations (e.g. horse racing, dogs) the following is an approximate description. At each trial a gambler bets $m, assumed fixed. With probability q he loses all the Sm and with...

A portion of a circular cylindrical shell forms a small vane which is welded to the vertical shaft AB. The vane and shaft rotate about the y axis with a constant angular velocity of 180 rpm...

Calculate the following using the information below: 1. portfolio expected return 2.Covariance of returns on bond and stock 3. Correlation Coefficient and what does it say 4.Standard deviation for...

Which of the following are not true about cost centers? Cost Center is an organizational unit in a Controlling Area representing a clearly delimited location where costs occur. None of the options...

One important aspect of learning from experience is observing the consequences of ones actions. Sometimes, however, the most significant consequences of a leaders actions do not occur for several...

With reference to Exercise 3.5, which of the pairs of events, $P$ and $Q, Q$ and $R, R$ and $S$, and $P$ and $S$, are mutually exclusive? Data From Exercise 3.5 3.5 To construct sample...

To construct sample spaces for experiments in which we deal with non-numerical data, we often code the various alternatives by assigning them numbers. For instance, if an engineer is asked to rate...

With reference to the sample space of Figure 3.1, express each of the following events in words. (a) $F=\{(1,0),(1,1)\}$ (b) $G=\{(0,2),(1,1),(2,0)\}$ (c) $F \cap G$ Data From Figure 3.1 Figure...

13.A system using Lamport timestamps executes the following run shown in below. Initially, all four processes start with sequence numbers containing all zeros. An arrow shows a message, and each...

PulseOlilkview AccessPoint @ Review Variance (2) ) Review Variance e Web Slice GalleryCensusWo D | Question 20 2 p The predetermined overhead rate is usually calculated O at the end of each month. O...

2. Draw a demand and supply diagram to show surplus and shortage