Sample z score. The z scale (or standard scale)

measures the position of a data point relative to the mean and in units of the standard deviation.

Specifically, When two measurements originate from different sources, converting them to the z scale helps to draw a sensible interpretation of their relative magnitudes. For instance, suppose a student scored 65 in a math course and 72 in a history course. These (raw) scores tell little about the student’s performance. If the class averages and standard deviations were s 20 in math and , s

10 in history, this student’s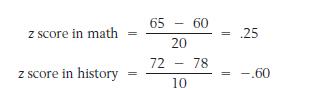

Thus, the student was .25 standard deviations above the average in math and .6 standard deviations below the average in history.

(a) If and s 120, find the z scores of 350 and 620.

(b) For a z score of 2.4, what is the raw score if and s 50?

z score in math = z score in history 65 - 60 20 .25 72 78 -.60 10