Use the discrete convolution formula, Theorem 6.10, to obtain the probability distribution of \(X+Y\) when \(X\) and \(Y\) are independent and each has the uniform distribution on \(\{0,1,2\}\).

Data From Theorem 6.10

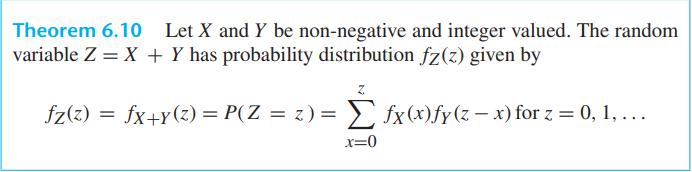
Theorem 6.10 Let X and Y be non-negative and integer valued. The random variable Z = X + Y has probability distribution fz(z) given by Z fz(z) = fx+y(z) fx+y (z) = P(Z = z) = fx(x)fy(z-x) for z = 0, 1, ... x=0