Question: Consider an (M / M / 1 / N) queue whose arrival and service rates are equal. Suppose that customers who join the queue receive

Consider an $M / M / 1 / N$ queue whose arrival and service rates are equal. Suppose that customers who join the queue receive a reward $R$ at the end of service, but pay at a rate of $C$ per unit time while they are waiting. Find inequalities that characterize the optimal waiting room size $N$ that maximizes the long-run expected profit per customer, per unit time:

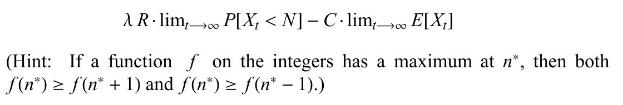
AR lim P[X,

Step by Step Solution

★★★★★

3.32 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Introduction To The Mathematics Questions!

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

Question: What as the average weekly safety inventory level of refined sugar from the beginning January 2022 to the end of July 2022? A. 512,465.9691 metric tons per week B. 316,002.1474 metric tons...

If you dissolve 8.14 grams of calcium chloride, CaCl 2 , in enough water to make 125.0 mL of solution, what is the molarity of the solution?

Historical data at a retail store (e.g. Wegmans, Giant, Safeway, Walmart, etc.) shows that the total average arrival rate of customers to checkout lanes (cashiers) at the store is 170 customers per...

(11) The average number of customers being served: r For nearly all queuing systems, there is a relationship between the average time a unit spends in the system or queue and the average number of...

Suppose that you need to decide on which machine to use for a process in your production. The parts arrive at the workstation for the process at a rate of 2 0 per hour and the time between...

U.S. Copyright Law (title 17 of U.S. code) governs the reproduction and redistribution of copyrighted material. Downloading this document for the purpose of redistribution is prohibited. Chapter 15...

From the book Networks, Crowds, and Markets: Reasoning about a Highly Connected World. By David Easley and Jon Kleinberg. Cambridge University Press, 2010. Complete preprint on-line at...

8. 10. In the model of Section 14, suppose that Cl is the exponential distribution with rate 4 and G: is exponential with rate 3. Suppose that the arrivals are according to a Poisson process with...

\fCHAPTER 14 Server Farms: M/M/k and M/M/k/k In today's high-volume world, almost no websites, compute centers, or call centers consist of just a single server. Instead a \"server farm\" is used. The...

June 1 2020 - Silverman was asking $258000 for land. 315,000 five year promissory note Interest - 4% (Paid annually on june 1 for next five yrs) Calculate the purchase price of the land, and Prepare...

A gardener wishes to put trees in their front yard. The height of the tree, y feet, t whereb is a constant. 10t - t+b years after planting the tree is given by y The gardener knows that after 6...

3 . Create a new table Employee consisting of a four - digit employee id , employee last name, employee first name, employee date of birth and employee hourly pay rate. The primary key for this table...

The dollar value of output in year 3 is higher than the dollar value of output in year 2 a. entirely because of price changes. b. entirely because of output changes. c. because of both price and...

If the mean plasma-aldosterone level in African American children was 230 pmol/L with a standard deviation of 203 pmol/L, then what percentage of African American children have levels 300 pmol/L if...

If the mean plasma-aldosterone level in Caucasian children is 400 pmol/L with standard deviation of 218 pmol/L, then what percentage of Caucasian children have levels 300 pmol/L if normality is...

The distribution of plasma-aldosterone concentration in 53 Caucasian and 46 African American children is shown in Figure 5.22. Does the assumption of normality seem reasonable? Why or why not? Figure...

What is the difference between method overloading and method overriding in Java? true or false

Find the number of 17 lb magnesium anodes and the spacing between the anode to protect a 10 000 ft of a bare 4" diameter pipeline in a corrosive soil having a resistivity of 800 ohms-cm. Assume a...

6 0 ) Who is considered the principal author of the Declaration of independence?