Let (left(p_{n} ight)_{n=0,1,2, ldots}) form a discrete probability mass function on the non-negative integers. Define the probability generating function of this distribution as the function

Let \(\left(p_{n}\right)_{n=0,1,2, \ldots}\) form a discrete probability mass function on the non-negative integers. Define the probability generating function of this distribution as the function

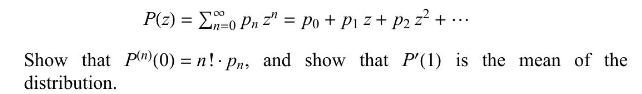
P(z) == Pnz" = Po + P z + P2 z + ... in=0 Show that P(0)=n! Pn, and show that P'(1) is the mean of the distribution.