A count random variable, say Y, takes on nonnegative integer values, {0, 1, 2, . . .}. The most common distribution for a count variable is the Poisson(θ) distribution, where the parameter u is the expected value: θ = E(Y). The probability density function is

It can be shown that Var(Y) = θ, so that the mean and variance are the same.

(i) For a random draw Yi from the population, find the log-likelihood function ℓ(θ; Y_i) = log[f(Y_i; θ)].

What is the log likelihood for a random sample of size n, say L_n(θ)?

(ii) Using the notational convention in Section C.7, find the first order condition for the MLE, u^

θ̂, and show that θ̂ = Y̅, the sample average.

(iii) Why is θ̂ unbiased?

(iv) Find Var(Y) as a function of u and n.

(v) Why is Y consistent?

(vi) Do the unbiasedness and consistency of the MLE in this case depend on whether the Poisson distribution is correct? Explain.

(vii) What is the distribution of

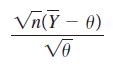
as n → ∞? Explain.

(viii) If E(Y) = θ but Var(Y) = v(θ) . 0—so that the Poisson distribution may fail—modify the random variable in (vii) so that it has a limiting distribution that does not depend on u.

f(y; 0) = exp(-0)0'ly!, y = 0, 1, 2, ... = 0 otherwise