Consider the log-linear regression model (ln (y)=beta_{1}+beta_{2} x+delta_{1} D+delta_{2}(x times D)+e). If the regression errors are normally
Question:
Consider the log-linear regression model \(\ln (y)=\beta_{1}+\beta_{2} x+\delta_{1} D+\delta_{2}(x \times D)+e\). If the regression errors are normally distributed \(N\left(0, \sigma^{2}\right)\), then \(E(y \mid x, D)\) is given in equation (XR7.11.1).
a. Find \(E(y \mid x, D=1)\) and \(E(y \mid x, D=0)\).
b. Show that
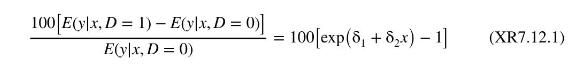
This is the percentage change in the expected value of \(y\), given \(x\), when the indicator variable changes from \(D=0\) to \(D=1\).
c. Given the log-linear model, the value of \(\ln (y)\) when \(D=0\) is \(\ln (y \mid D=0, x)=\beta_{1}+\beta_{2} x+e\), and when \(D=1\) we have \(\ln (y \mid D=1, x)=\left(\beta_{1}+\delta_{1}\right)+\left(\beta_{2}+\delta_{2}\right) x+e\). Subtract \(\ln (y \mid D=0, x)\) from \(\ln (y \mid D=1, x)\), and multiply by 100 , to obtain
![]()
d. A fitted log-linear model for house price, where \(S Q F T(x)\) is the house's living area (100s of square feet) and \(U T O W N(D)\) is an indicator variable with \(U T O W N=1\) for houses near a university, and zero otherwise, is
![]()
Calculate the percentage change in the expected value of PRICE for a house of 2500 square feet using (XR7.12.1). Also calculate the approximate value in (XR7.12.2).
e. If \(d_{1}\) and \(d_{2}\) are the least squares estimators of \(\delta_{1}\) and \(\delta_{2}\) in equation (XR7.12.2), write down the formula for the standard error of \(100\left(d_{1}+d_{2} x\right)\), given \(x\).
f. Let \(\lambda=100\left[\exp \left(\delta_{1}+\delta_{2} x\right)-1\right]\) and \(\hat{\lambda}=100\left[\exp \left(d_{1}+d_{2} x\right)-1\right]\). Use Derivative Rule 7 to show that \(\partial \lambda / \partial \delta_{1}=100 \exp \left(\delta_{1}+\delta_{2} x\right)\) and \(\partial \lambda / \partial \delta_{2}=100 \exp \left(\delta_{1}+\delta_{2} x\right) x\). The "delta method" for finding the variance of a nonlinear function, such as \(\hat{\lambda}\), is discussed. Using the delta method, write out the expression for standard error of \(\hat{\lambda}\).
Data From Equation XR7.11.1:-
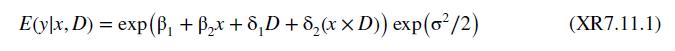
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





