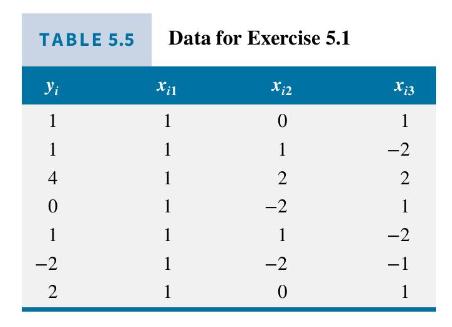
Question: Consider the multiple regression model with the seven observations on (y_{i}, x_{i 1}, x_{i 2}), and (x_{i 3}) given in Table 5.5. Use a hand
Consider the multiple regression model
![]()
with the seven observations on \(y_{i}, x_{i 1}, x_{i 2}\), and \(x_{i 3}\) given in Table 5.5.
Use a hand calculator or spreadsheet to answer the following questions:
a. Calculate the observations in terms of deviations from their means. That is, find \(x_{i 2}^{*}=x_{i 2}-\bar{x}_{2}\), \(x_{i 3}^{*}=x_{i 3}-\bar{x}_{3}\), and \(y_{i}^{*}=y_{i}-\bar{y}\).
b. Calculate \(\sum y_{i}^{*} x_{i 2}^{*}, \sum x_{i 2}^{* 2}, \sum y_{i}^{*} x_{i 3}^{*}, \sum x_{i 2}^{*} x_{i 3}^{*}\), and \(\sum x_{i 3}^{* 2}\).
c. Use the expressions in Appendix \(5 \mathrm{~A}\) to find least squares estimates \(b_{1}, b_{2}\), and \(b_{3}\).
d. Find the least squares residuals \(\hat{e}_{1}, \hat{e}_{2}, \ldots, \hat{e}_{7}\).
e. Find the variance estimate \(\hat{\sigma}^{2}\).
f. Find the sample correlation between \(x_{2}\) and \(x_{3}\).
g. Find the standard error for \(b_{2}\).
h. Find \(S S E, S S T, S S R\), and \(R^{2}\).
y = x+x2 + x 13 3 + ei
Step by Step Solution
3.57 Rating (147 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


