(i) Consider the simple regression model y = 0 + 1 x + u under the first four Gauss-Markov assumptions. For some function

(i) Consider the simple regression model y = β₀ + β₁x + u under the first four Gauss-Markov assumptions. For some function g(x), for example g(x) = x² or g(x) = log(1 + x²) , define z_i = g(x_i). Define a slope estimator as

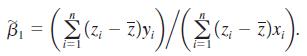
Show that β̂₁ 1 is linear and unbiased. Remember, because E(u|x) = 0, you can treat both x_i and z_i as nonrandom in your derivation.

(ii) Add the homoskedasticity assumption, MLR.5. Show that

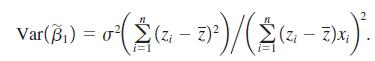
(iii) Show directly that, under the Gauss-Markov assumptions, Var (β̂₁) ≤ Var (β̂₁) where β̂₁ is the OLS estimator. The Cauchy-Schwartz inequality in Math Refresher B implies that

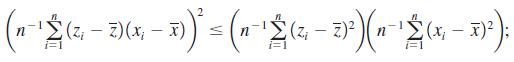
notice that we can drop x from the sample covariance.

z)x;