Using the data file usmacro, estimate the (operatorname{AR}(1)) model (G_{t}=alpha+phi G_{t-1}+v_{t}). From these estimates and those obtained
Question:
Using the data file usmacro, estimate the \(\operatorname{AR}(1)\) model \(G_{t}=\alpha+\phi G_{t-1}+v_{t}\). From these estimates and those obtained in Exercise 9.16, use the results from Exercise 9.4 to find point and \(95 \%\) interval forecasts for \(U_{2016 Q 2}, U_{2016 Q 3}\), and \(U_{2016 Q 4}\).
Data From Exercise 9.4:-
Consider the ARDL \((2,1)\) model
![]()
with auxiliary AR(1) model \(x_{t}=\alpha+\phi x_{t-1}+v_{t}\), where \(I_{t}=\left\{y_{t}, y_{t-1}, \ldots, x_{t}, x_{t-1}, \ldots\right\}, E\left(e_{t} \mid I_{t-1}\right)=0\), \(E\left(v_{t} \mid I_{t-1}\right)=0, \operatorname{var}\left(e_{t} \mid I_{t-1}\right)=\sigma_{e}^{2}, \operatorname{var}\left(v_{t} \mid I_{t-1}\right)=\sigma_{v}^{2}\), and \(v_{t}\) and \(e_{t}\) are independent. Assume that sample observations are available for \(t=1,2, \ldots, T\).
a. Show that the best forecasts for periods \(T+1, T+2\) and \(T+3\) are given by
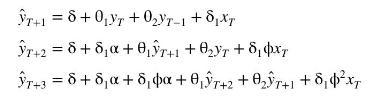
b. Show that the variances of the forecast errors are given by
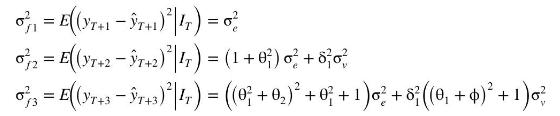
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





