a. Let {v₁; v_2,.......,v_p} be linearly independent set of vectors in Rⁿ that is not necessarily orthogonal. Describe how to find the best approximation to z in Rⁿ by vectors in W = Span{v₁; v₂,.......,v_p} without first constructing an orthogonal basis for W.

b. Let

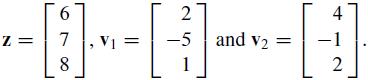
Find the best approximation to z by vectors in Span {v₁, v₂} using part (a) and using the orthogonal basis found in Exercise 3 in Section 6.4. Compare.

Data From Exercise 3 in Section 6.4

The given set is a basis for a subspace W. Use the Gram–Schmidt process to produce an orthogonal basis for W.

Transcribed Image Text:

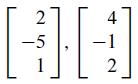
6 Z= 7 8 V1 2 -5 1 and V2 -1 2