Example 2 in Section 4.8 displayed a low-pass linear filter that changed a signal {y_k} into {y_k+1} and changed a higher-frequency signal {ωk} into the zero signal, where y_k = cos(πk/4) and (ω_k) = cos(3πk/4). The following calculations will design a filter with approximately those properties. The filter equation is

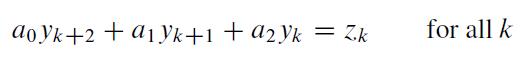
Write an equation Ax = b, where A is a 16 x 3 matrix formed from the two coefficient matrices above and where b in R¹⁶ is formed from the two right sides of the equations. Find a₀, a₁, and a₂ given by the least-squares solution of Ax = b. (The .7 in the data above was used as an approximation for √2/2, to illustrate how a typical computation in an applied problem might proceed. If .707 were used instead, the resulting filter coefficients would agree to at least seven decimal places with √2/4; 1/2, and √2/4, the values produced by exact arithmetic calculations.)

Data From Example 2 in Section 4.8

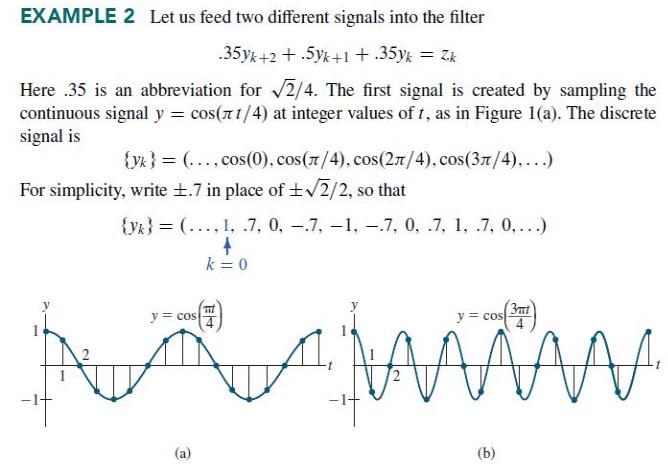
aoyk+2a1Yk+1 + ayk = Zk for all k