Question: Given u 0 in R n , let L = Span {u}. For y in R n , the reflection of y in L

Given u ≠ 0 in Rⁿ, let L = Span {u}. For y in Rⁿ, the reflection of y in L is the point refl_L, y defined by

refl, y = 2 proj, y - y

See the figure, which shows that refl_L ŷ = proj_L, y and ŷ - y. Show that the mapping y ↦ refl_L, y is a linear transformation.

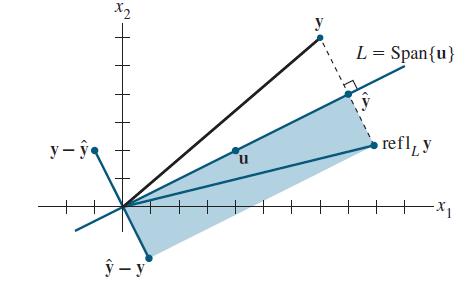
The reflection of y in a line through the origin.

refl, y = 2 proj, y - y

Step by Step Solution

★★★★★

3.45 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To show that the mapping y reflL y is a linear transformation we need to prove that it satisfies two properties additivity and scalar multiplication Lets consider two vectors y and y in R and a scalar ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Linear Algebra And Its Applications Questions!

Let L1 : U V and L2 : V W be linear transformations, and let L = L2 L1 be the mapping defined by L(u) = L2(L,(u)) for each u U. Show that L is a linear transformation mapping U into W

Let f: Rn Rm be a matrix transformation defined by f(u) = Au, where A is an m x n matrix. (a) Show that f(u + v) = f(u) + f(v) for any u and v in Rn. (b) Show that f(cu) = cf(u) for any u in Rn and...

Let f: Rn Rm be a matrix transformation defined by f(u) = Au, where A is an m x n matrix. Show that if u and v are vectors in Rn such that f(u) = 0 and f(v) = 0, where Then f(cu + dv) = 0 for any...

854 CHAPTER 15 DIFFERENTIATION IN SEVERAL VARIABLES 9. 20. Jessica and I at 2 oh ; h (x , y ) = -, x = 1/2, y = 1712 paths that make a with velocity va 10. "J : f ( x , y , Z ) = xy - 22, x = rcos0,...

Question 1 [10 points] Determine the values of a for which the following system of linear equations has no solutions, a unique solution, or infinitely many solutions. You can select 'always',...

History Bookmarks Profiles Tab Window Help Col Cox [Sc 1 1 Inb Sun Dec 11 10:42 PM Ath C Eth C Eth - (28 C Co bio Cri \\ Par how @ car C Ic college.blackboard.com/ultra/courses/_114529_1/cloutline ch...

Considerations for Employee Benefit Programs that Benefit Employers and Employees Lee P olk Employers must compete in the marketplace for talented employ ees at every levelboth in recruitment and...

puzzle1.txt W D B M J Q D B C J N Q P T I I R Z U X U Z E A O I O R T N M N Z P L R N H L Y L X H M D M Y E K A I D P I U L Y O W I A O A B A R K U F V I H L A A L O N M R X K I O J N A V R N A E P T...

Feather Friends, Inc., distributes a high-quality wooden birdhouse that sells for $120 per unit Variable expenses are $60.00 per unit, and fixed expenses total $180,000 per year. Its operating...

A cylindrical capacitor contains an inner conducting solid Q) and an outer conducting shell (-Q) separated by an insulator. Both have a charge magnitude of 2.00 x 10 1C. Radius a 0.0200m and radius...

Gestalt. Inc. uses a kanban system in its automobile production facility in Germany. This facility operates 8 hours per day to produce the Jitterbug, a replacement for the obsolete but immensely...

=+3.42 According to the National Association of Home Builders, the average size of a home in 1950 was 983 ft2 . The average size increased to 1500 ft2 in 1970, 2080 ft2 in 1990; and 2330 ft2 in 2003...

What is the center of your simulated null distribution? Does it make sense that this is the center? Explain.

Are there any values of simulated sample proportions that are less than 0.10? Are there any values of simulated sample proportions that are greater than 0.10? What does that tell you?

What proportion of San Luis Obispo (SLO) residents dine at restaurants at least once a week? To investigate, a local high school student, Deidre, decides to conduct a survey. She selects a random...

Consider where you currently work, where you have previously worked, or a well-known company where you would like to work. How might this company make capital investment decisions? What capital...

EMPLOYEE TERMINATION PAYMENT Damon was born on 11 April 1961 and was 58 years of age when he was made redundant on 12 June 2019. His year to date earnings up to that date were $190,000. In addition...

> Question 34 Acer Inc. sells two types of computer hard drives: S Drive and S+ Drive. The sales mix is 30% (S Drive) and 70% (S+ Drive). The S Drive has variable costs per unit of $90 and a selling...