Let g(t) be defined as in Exercise 25. Its graph is called a quadratic Bzier curve, and it is used in some computer graphics designs.

Let g(t) be defined as in Exercise 25. Its graph is called a quadratic Bézier curve, and it is used in some computer graphics designs. The points p₀, p₁, and p₂ are called the control points for the curve. Compute a formula for g(t) that involves only p₀, p₁, and p₂. Then show that g(t) is in conv {p₀; p₁; p₂} for 0 ≤ t ≤ 1.

Data From Exercise 25

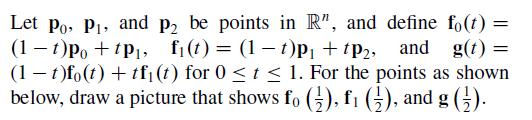
Let Po, P, and p2 be points in R", and define fo(t) = (1 t)Po +tP, f(t) = (1-t)p + tp, and g(t) = (1 t)fo(t) + tf (t) for 0 t 1. For the points as shown below, draw a picture that shows fo (), f (2), and g ().