Let u₁ and u₂ be as in Exercise 19, and let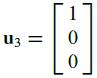

It can be shown that u₄ is not in the subspace W spanned by u₁ and u₂. Use this fact to construct a nonzero vector v in R³ that is orthogonal to u₁ and u₂.

Data from in Exercises 19

Let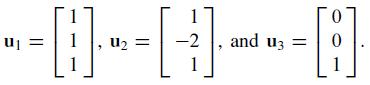

Note that u₁ and u₂ are orthogonal but that u₃ is not orthogonal to u₁ or u₂. It can be shown that u₃ is not in the subspace W spanned by u₁ and u₂. Use this fact to construct a nonzero vector v in R³ that is orthogonal to u₁ and u₂.

0 0 = n 1