Question: Solve the initial value problem x'(t) = Ax(t) for t 0, with x(0) = (3,2). Classify the nature of the origin as an attractor,

Solve the initial value problem x'(t) = Ax(t) for t ≥ 0, with x(0) = (3,2). Classify the nature of the origin as an attractor, repeller, or saddle point of the dynamical system described by x' = Ax. Find the directions of greatest attraction and/or repulsion. When the origin is a saddle point, sketch typical trajectories.

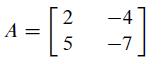
A || 2 5 -4 -7

Step by Step Solution

★★★★★

3.49 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

13 3 3 1 For 4 31010 For 6 det 41210 24 24260 Eigenvalues 4 and 6 1 3 x1 1 3 0 1 Vx0 1 13 0 0 0 For ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Linear Algebra And Its Applications Questions!

In Exercises 3-6, solve the initial value problem x'(t) = Ax(t) for t > 0, with x(0) = (3, 2). Classify the nature of the origin as an attractor, repeller, or saddle point of the dynamical system...

Solve the initial value problem x'(t) = Ax(t) for t 0, with x(0) = (3,2). Classify the nature of the origin as an attractor, repeller, or saddle point of the dynamical system described by x' = Ax....

The inputs for this scenario would involve the helicopters and the aids loaded in the helicopters for the Physician (DR) hours per week Aide (PA) hours per week 40 60 80 30 200 300 360 40 400 550 600...

Solve the initial value problem x t Ax t for t20 with x 0 5 2 Classify the nature of the origin as an attractor repeller or saddle point of the dynamical system described by x Ax Find the directions...

Solve the initial value problem x'(t) = Ax(t) for t2 0, with x(0) = (3,2). Classify the nature of the origin as an attractor, repeller, or saddle point of the dynamical system described by x' = Ax....

I am having trouble with this question. I am getting really complicated eigen values and I am not sure how to handle them. Also I am having trouble with drawing the graph at the end. Solve the...

2x (b) f" (2) = - (1 + x2)2 + sin(2), f'(0) = 2 and f(0) = -1, find f (x) . (4) (4 marks) In questions 4a-4b, find the value or a formula for the given sum. (a) (i - 1) (2+ 2). i= 1 199 (b) sin(,)(3)...

Solve the initial value problem x'(t) = Ax(t) for t2 0, with x(0) = (1,5). Classify the nature of the origin as an attractor, repeller, or saddle point of the dynamical system described by x' = Ax....

1. Solve the equation. dy = 5x4 (6 +12 ) 2 7. solve the following differential equation. (16y2 - xy) dx +x2 dy= 0 2. Solve the initial value problem. 8. solve the following differential equation. x2...

Please answer these four questions. Apply the method of undetermined coefficients to find the particular solution to the following system that satisfies the given initial conditions. x' = 2x + 4y +...

Gold Corp., a Canadian public corporation, carries on business in Canada. For the current year, Gold Corp. has manufacturing and processing profits (M&P) of $300,000, calculated in accordance with...

2.11.2.2f) determine (f) als z = Intg

How do operational information systems differ from managerial systems?

7.85 Measures of nerve conductivity are used in the diagnosis of certain medical conditions. The paper Effects of Age, Gender, Height, and Weight on Late Responses and Nerve Conduction Study...

Find EPPI, EMV*, and EVPI for the accompanying payoff table and probabilities. P(s 1 ) = .10 P(s 2 ) = .25 P(s 3 ) = .50 P(s 4 ) = .15 a, 75 60 110 S2 40 110 150 220 120 85 S3 250 120 130 S4

For Exercise 22.17, determine the opportunity loss table and compute EOL*. Confirm that EOL* = EVPI. In exercise 22.17 Find EPPI, EMV*, and EVPI for the accompanying payoff table and probabilities....

Given the following payoff table and probabilities, determine EVPI. P(s 1 ) = .5 P(s 2 ) = .5 az az a4 a1 45 30 65 20 110 70 95 S2

need help for all septemebrs Bayside Cinema Company owns movie theatres. Bayside Cinema engagad in the following trant (i) (Click on the link to viow the transactions.) Bayside uses the following...

Walsh Company manufactures and sells one product. The following information pertains to each of the company's first two years of operations: Variable costs per unit: Manufacturing: Direct materials...

Garden Depot is a retailer that is preparing its budget for the upcoming fiscal year. Management has prepared the following summary of its budgeted cash flows: Total cash receipts 1st Quarter 2nd...