Boyle (1988) proposed the following three-jump process for the approximation of the asset price process over one
Question:
Boyle (1988) proposed the following three-jump process for the approximation of the asset price process over one period:
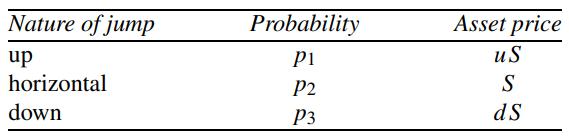
where S is the current asset price. The middle jump ratio m is chosen to be 1. There are five parameters in Boyle’s trinomial model: u,d and the probability values. The governing equations for the parameters can be obtained by:
(i) Setting the sum of probabilities to be 1; and
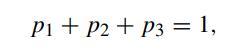
(ii) Equating the first two moments of the approximating discrete distribution and the corresponding continuous lognormal distribution
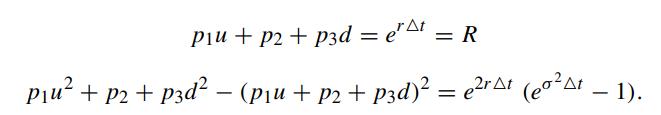
The last equation can be simplified as
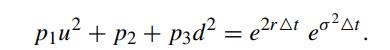
The remaining two conditions can be chosen freely. They were chosen by Boyle (1988) to be

By solving the five equations together, show that
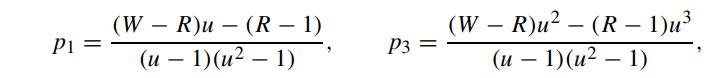
where W = R2eσ2Δt. Also show that Boyle’s trinomial model reduces to the Cox–Ross–Rubinstein binomial scheme when λ = 1.
Step by Step Answer:






