Consider a typical term in g(x,t) where can be either 2n(u ) or 2 2n(u ) Show that the above term can be rewritten as Hence, show that Use the above result to derive the price formula of the European double knockout call option c o LU see Sect 4 1 3 We generalize the barriers to become exponential ...

The Answer is in the image, click to view ...

Consider a typical term in g(x,t) where can be either 2n(u ) or 2 +

Question:

Consider a typical term in g(x,t)

exp( 44) exp( - 2017). 202 (x - )2 221

where ξ can be either 2n(u − ℓ) or 2ℓ + 2n(u − ℓ). Show that the above term can be rewritten as

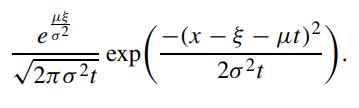
eo 221 exp -(x - - ut) . 201

Hence, show that

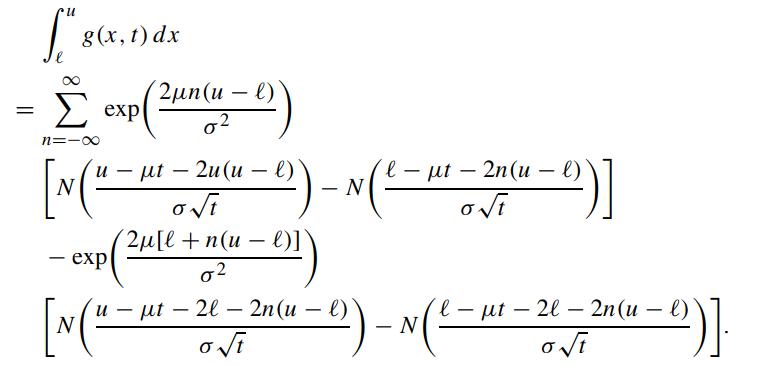
= f" 8(x g(x, t) dx exp n=- - - 2u(u - l) l - - 2n(u l) [x("0 3014 12)-N( 2 300) N - exp (2n(u - l) 02 2[l

Use the above result to derive the price formula of the European double knockout call option c^o_LU [see Sect. 4.1.3].

We generalize the barriers to become exponential functions in time. Suppose the upper and lower barriers are set to be Ue^δ1tand Le^δ2t ,t ∈ [0,T ]. Here, δ₁ and δ₂ are constant parameters and the barriers do not intersect over [0,T ]. Show that the price formula of the European double knock-out call option can be expressed as (Kunitomo and Ikeda, 1992)

$CLU= = S where n=- {(F)"(5) - (US) - - Xe-T d = d3 Ln+1 3-2 Uns [N(d3) - N(d4)] Un 141-2 L {( {()^ (5) **$