Let W n (S; X) = lim e r Un(S, ; X), where U

Let W_n^∞ (S; X) = lim_τ→∞ e^rτUn(S, τ ; X), where U_n(S, τ; X) is the value of the n-reset put option [see (5.4.20)]. For r n^∞ (S) is given by (Dai, Kwok and Wu, 2003)

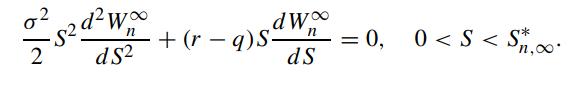
The auxiliary conditions are given by 

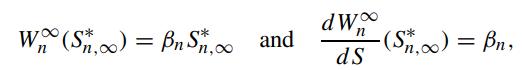
where β_n = W^∞_n−1(1; 1). Show that

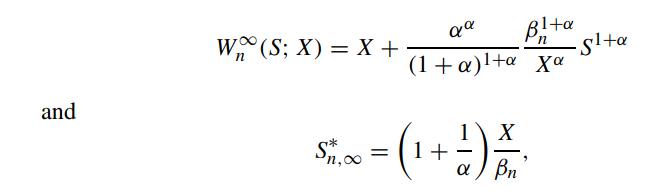
where α = 2(q − r)/σ². The recurrence relation for β_n is deduced to be

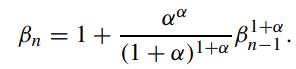Show that β₁ = 1 and lim_n→∞ β_n = 1 + 1/α . Also, find the first few values of S^∗_n,_∞. 

Transcribed Image Text:

N|9 n -S2d²wx ds² dw% n ds + (r-q)s- = 0, 0