The penalty method is characterized by the replacement of the linear complementarity formulation of the American option model by appending a nonlinear penalty term in the Black–Scholes equation. Let h(S) denote the exercise payoff of an American option. The nonlinear penalty term takes the form ρ max(h − V, 0), where ρ is the positive penalty parameter and V (S,τ) is the option price function. It can be shown that when ρ → ∞, the solution of the following equation 

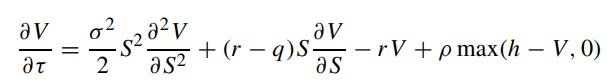
gives the solution of the American option price function. Discuss the construction of the Crank–Nicolson scheme for solving the above nonlinear differential equation, paying special attention to the solution of the resulting nonlinear algebraic system of equations. Note that the nonlinearity stems from the penalty term (Forsyth and Vetzal, 2002).

Transcribed Image Text:

av ат = ชุด 5202 v მ S2 2 + (r= q)so av as rV + p max(h - V, 0)