In the Hückel treatment of the cyclopropenyl radical, the basis functions are the three 2pz atomic orbitals,
Question:
ψ = c1 f1 + c2 f2 + c3 f3.
The possible values of the orbital energyWare sought as a function of the c coefficients by solving the three simultaneous equations
xc1 + c2 + c3 = 0,
c1 + xc2 + c3 = 0,
c1 + c2 + xc3 = 0,
where x = (α ˆ’ W)/β) and where α and β are certain integrals whose values are to be determined from empirical data.
(a) The determinant of the c coefficients must be set equal to zero in order for a nontrivial solution to exist. This is the secular equation. Solve the secular equation and obtain the orbital energies.
(b) Solve the three simultaneous equations, once for each value of x. Since there are only two independent equations, express c2 and c3 in terms of c1.
(c) Impose the normalization condition c21 + c22 + c23 = 1 to find the values of the c coefficients for each value of W.
(d) Check your work by using Mathematica to find the eigenvalues and eigenvectors of the matrix
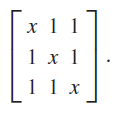
Step by Step Answer:






