Approximation of (sigma)-algebras. Let (mathscr{G}) be a Boolean algebra in (X), i.e. a family of sets such
Question:
Approximation of \(\sigma\)-algebras. Let \(\mathscr{G}\) be a Boolean algebra in \(X\), i.e. a family of sets such that \(X \in \mathscr{G}\) and \(\mathscr{G}\) is stable under the formation of finite unions, intersections and complements. Let \(\mathscr{A}=\sigma(\mathscr{G})\) and \(\mu\) be a finite measure on \((X, \mathscr{A}, \mu)\). Let \(A \triangle B:=(A \backslash B) \cup(B \backslash A)\) denote the symmetric difference of \(A, B \subset X\).
(i) For every \(\epsilon>0\) and \(A \in \mathscr{A}\) there is some \(G \in \mathscr{G}\) such that \(\mu(A \triangle G) \leqslant \epsilon\).
[ \(\{A \in \mathscr{A}: \forall \epsilon>0 \exists G \in \mathscr{G}: \mu(A \triangle G) \leqslant \epsilon\}\) is a Dynkin system.]
(ii) Let \(\mu, u\) be finite measures on \((X, \mathscr{A})\). For every \(\epsilon>0\) and \(A \in \mathscr{A}\) there is some \(G \in \mathscr{G}\) such that \(\mu(A \triangle G) \leqslant \epsilon\) and \(u(A \triangle G) \leqslant \epsilon\).
(iii) Assume that \(X=\mathbb{R}^{n}, \mathscr{A}=\mathscr{B}\left(\mathbb{R}^{n}ight)\) and \(\mu=\lambda^{n}\). A set \(A \in \mathscr{A}\) satisfies \(\mu(A)=0\) if, and only if, for every \(\epsilon>0\) there is a sequence \(\left(I_{n}ight)_{n \in \mathbb{N}} \subset \mathscr{J}\), such that \(A \subset \bigcup_{n} I_{n}\) and \(\mu\left(\bigcup_{n} I_{n}ight) \leqslant \epsilon\).
Remark. Compare the result of this exercise with Theorem 27.25 .
Data from theorem 27.25

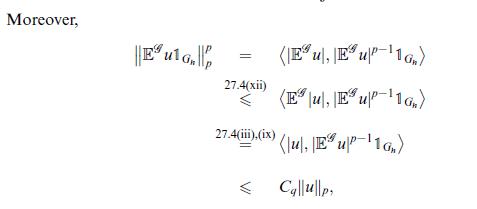

Step by Step Answer:






