Assume that (u in L^{1}left(lambda^{1}ight) cap L^{infty}left(lambda^{1}ight)) and (widehat{u} geqslant 0). Show that (widehat{u} in L^{1}left(lambda^{1}ight)). Extend

Question:

Assume that $u \in L^{1}\left(\lambda^{1}ight) \cap L^{\infty}\left(\lambda^{1}ight)$ and $\widehat{u} \geqslant 0$. Show that $\widehat{u} \in L^{1}\left(\lambda^{1}ight)$. Extend the assertion to $u \in L^{2}\left(\lambda^{1}ight)$

[estimate $\int \widehat{u} \widehat{g}_{t} d \xi$, where $g_{t}$ is as in Example 19.2 (iii) Use monotone convergence for the limit $t ightarrow 0$.]

Data from example 19.2 (iii)

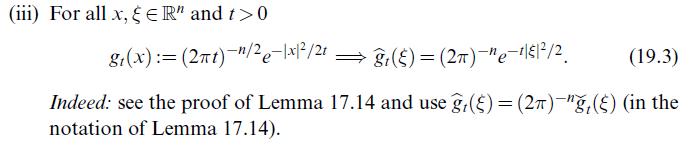
(iii) For all x, & ER" and t> 0 (19.3) Indeed: see the proof of Lemma 17.14 and use g() = (27)-,() (in the