Construct an example showing that for \(u, w \in \mathcal{M}^{+}(\mathscr{B})\) the equality \(\int_{B} u d \mu=\int_{B} w d \mu\) for all \(B \in \mathscr{B}\) does not necessarily imply that \(u=w\) almost everywhere.

[ in view of Corollary \(\left.11.7 \muight|_{\mathscr{B}}\) cannot be \(\sigma\)-finite. Consider on \((\mathbb{R}, \mathscr{B}(\mathbb{R}))\) the measure \(\mu=m \lambda^{1}\), where \(m=\mathbb{1}_{\{|x| \leqslant 1\}}+\infty \mathbb{1}_{\{|x|>1\}}, u \equiv 1\) and \(w=\mathbb{1}_{\{|x| \leqslant 1\}}+2 \mathbb{1}_{\{|x|>1\}}\). Then all Borel subsets of \(\{|x|>1\}\) have \(\mu\)-measure either 0 or \(+\infty\), thus \(\int_{B} u d \mu=\int_{B} w d \mu\) for all \(B \in \mathscr{B}(\mathbb{R})\) while \(\mu(u eq w)=\infty\).]

Data from corollary 11.7

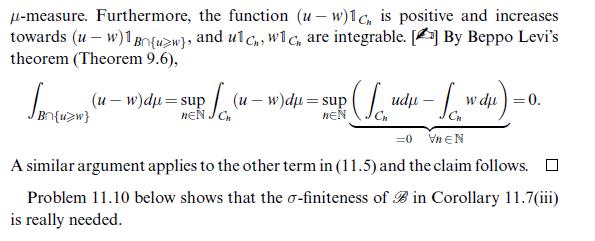
*Corollary (i) Ifu, w (ii) If u, w 11.7 Let BCA be a sub-o-algebra. L (B) and if fBudu=fB w du for all Be B, then u=w -a.e. M+ (B) and if fu du = fgw du for all BEB, then u=w -a.e. under the additional assumption that pl is o-finite. Proof (1) Since u and w are B-measurable, we have that Bn {u>w} and that Bn{u w} Jantinang (1 - 1)du - ( Jan (waw) " Bn{u>w} n{u w} by the linearity of the integral and our assumption. The other term on the right- hand side of (11.5) can be treated similarly, and the conclusion follows from Theorem 9.6(i). (ii) If u, w are positive measurable functions, we cannot use the linearity of the integral in (11.6) as this may yield an expression of the form '-0. We can avoid this by an approximation procedure which relies on the fact that is o-finite. Pick a sequence (Bn)neN CB with Bn X and (B) w} B,n{u 1), say [2]. 3 That is there exists an exhausting sequence (Br), C with B X and (B)