Define \(\phi: \mathbb{R} ightarrow \mathbb{R}\) by \(\phi(x):=(1-\cos x) \mathbb{1}_{[0,2 \pi)}(x)\), let \(u(x):=1, v(x):=\phi^{\prime}(x)\) and \(w(x):=\int_{(-\infty, x)} \phi(t) d t\). Then

(i) \(u \star v(x)=0\) for all \(x \in \mathbb{R}\);

(ii) \(v \star w(x)=\phi \star \phi(x)>0\) for all \(x \in(0,4 \pi)\);

(iii) \((u \star v) \star w \equiv 0 eq u \star(v \star w)\).

Does this contradict the associativity of the convolution which is implicit in Theorem 15.6 ?

Data from problem 15.6

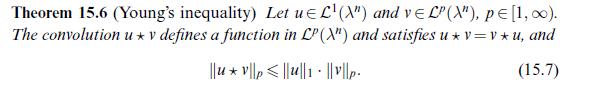
Theorem 15.6 (Young's inequality) Let ue L (X") and vELP(X"), p= [1,00). The convolution uv defines a function in LP (X") and satisfies u* v=v*u, and ||uv|p|u||1||v||p. (15.7)