Question: (i). Find examples showing that (f(A cap B) eq f(A) cap f(B)) and (f(A backslash B) eq f(A) backslash f(B)). In both relations one inclusion

(i). Find examples showing that $f(A \cap B) eq f(A) \cap f(B)$ and $f(A \backslash B) eq f(A) \backslash f(B)$. In both relations one inclusion ' $C$ ' or ' $\supset$ ' is always true. Which one?

(ii).Prove (2.6).

Equation 2.6

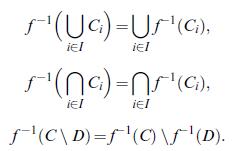
$S(UG)=US(c), El iEl f'(na)=n(a), EI El f'(C\D)=f(C) \ (D).$

S(UG)=US(c), El iEl f'(na)=n(a), EI El f'(C\D)=f(C) \ (D).

Step by Step Solution

★★★★★

3.31 Rating (139 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

i ii The inclusion fAn B c fAn fB is always true since AnB CA and An B C B imply that fAn B c fA a... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Measures Integrals And Martingales Questions!

Question 3 VO Limited is a clothing manufacturer carrying on business in Hong Kong. Its profits and loss accounts for the year ended 30 June 2018 are as follows: Income Sales gross profits - sales to...

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-6. On December 12, Irene purchased the building where her store is located. She paid...

Case Study: Quick Fix Dental Practice Technology requirements Application must be built using Visual Studio 2019 or Visual Studio 2017, professional or enterprise. The community edition is not...

James Simmons MAT-121-GS009 Assignment 6 Written Assignment 6 Answer all assigned exercises, and show all work. An asterisk indicates an exercise for which a graph pool is provided in the assignment...

I found some questions in which i have doubts. Please answer in detail along with diagram or graph where needed. And first question that i pointed with black circle, please give detailed explanation...

%% Lab 2 - Your Name - MAT 275 Lab %% Example code % Example 1 % NOTE: Delete examples before submission. A = [1 0; 0 -1] A = [1, 0; 0, -1] % NOTE: The two matrices above are the same. We can...

Hello, I need someone to please complete this financial Project. Below i have all the requirements and things that must be done. The company that the project's financial data is based on is Xerox and...

A discrete sequence {xn} can be converted into a continuous representation x(t) = ts X n= (t n ts) xn, where ts is the sampling period. (a) State two characteristic properties of Dirac's function. [2...

ID Salary 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 59.3 26.5 34.1 56.3 46.8 79.5 41.2 23.6 76 22.7 23.8 62.9 41.4 22.3 23.1 46.6 67.6 33.8 24 35 75.2 51.5 22.1 55.4 24.9 24.3 42.9 76.6 75.4...

What issues would you have to think about in going global with the new service that you developed in the questions above? How would you change your marketing mix to address those issues?

The following information was reported in the December 31 financial statements of National Airways, Incorporated (listed alphabetically, amounts in millions). Accounts Payable. Accounts Receivable...

Exhibit 14.2 showed the following information on cash and cash equivalents for Lemmons Company: Required: Calculate the change in cash. Net Changes Assets Cash 20X1 $70,000 20X2 Debit $175,000...

11.1 Is it both desirable and possible to harmonize company financial reporting in the European Union?

Let $B_{t}=\left(b_{t}, \beta_{t}ight), t \geqslant 0$, be a two-dimensional Brownian motion. a) Show that $W_{t}:=\frac{1}{\sqrt{2}}\left(b_{t}+\beta_{t}ight)$ is a $\mathrm{BM}^{1}$. b) Are...

Use Lemma 2.8 to show that (all finite dimensional distributions of) a $\mathrm{BM}^{d}$ is invariant under rotations. 2.8 Lemma. Let (X+)to be a d-dimensional stochastic process. X satisfies...

Let ( F t ) t 0 ( F t ) t 0 and ( G t ) t 0 ( G t ) t 0 be any two filtrations and define F = ( t 0 F t ) F = ( t 0 F t ) and G = ( t 0 G t ) G = ( t 0 G t ) . Show that Ft Gt (Vt...

Read and discuss Section 409 from the Sarbanes-Oxley Act of 2002. Discuss whether or not this section supports real time financial reporting?

Si los balances comparativos indican documentos por cobrar de $30,000 en el ao 1 y $40,000 en documentos por cobrar en el ao 2, el porcentaje de aumento es 25% 10% 70% 33,33%

Harry has two jobs. He earns $117,700 from his first job and $10,000 from his second job. How much total FICA withholding will Harry have withheld from his wages from working two jobs?