Question: In Example 12.15 we introduced Euler's gamma function: [Gamma(t)=int_{(0, infty)} x^{t-1} e^{-x} lambda^{1}(d x)] Show that (Gammaleft(frac{1}{2}ight)=sqrt{pi}). Data from example 12.15 Example 12.15 (Euler's gamma
In Example 12.15 we introduced Euler's gamma function:
\[\Gamma(t)=\int_{(0, \infty)} x^{t-1} e^{-x} \lambda^{1}(d x)\]
Show that \(\Gamma\left(\frac{1}{2}ight)=\sqrt{\pi}\).
Data from example 12.15
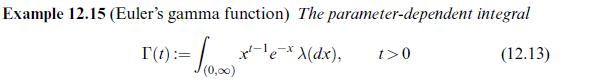
Example 12.15 (Euler's gamma function) The parameter-dependent integral ) := (0.00)*x^- e- x x (dx), (12.13) T(t):= t>0
Step by Step Solution
★★★★★
3.29 Rating (158 Votes )
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock
We have T 00 r 2 y12 e ... View full answer
Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock
Study Help