Let \(u: \mathbb{R}^{2} ightarrow[0, \infty]\) be a measurable function. \(S[u]:=\{(x, y): 0 \leqslant y \leqslant u(x)\}\) is the set above the abscissa and below the graph \(\Gamma[u]:=\{(x, u(x)): x \in \mathbb{R}\}\).

(i) Show that \(S[u] \in \mathscr{B}\left(\mathbb{R}^{2}ight)\).

(ii) Is it true that \(\lambda^{2}(S[u])=\int u d \lambda^{1}\) ?

(iii) Show that \(\Gamma[u] \in \mathscr{B}\left(\mathbb{R}^{2}ight)\) and that \(\lambda^{2}(\Gamma[u])=0\).

[ (i) use Theorem 8.8 to approximate \(u\) by simple functions \(f_{n} \uparrow u\). Thus we have \(S[u]=\bigcup_{n} S\left[f_{n}ight]\) and it is easy to see that \(S\left[f_{n}ight] \in \mathscr{B}\left(\mathbb{R}^{2}ight)\); alternatively, use Theorem 14.17 , set \(U(x, y):=(u(x), y)\) and observe that \(S[u]=U^{-1}(C)\) for the closed set \(C:=\{(x, y)\) : \(x \geqslant y\}\); (ii), (iii) use Tonelli's theorem.]

Data from theorem 14.17

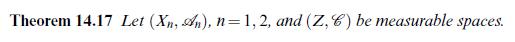
i.

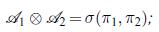
ii.

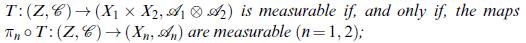
iii.

Transcribed Image Text:

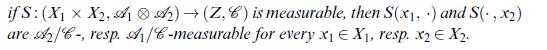
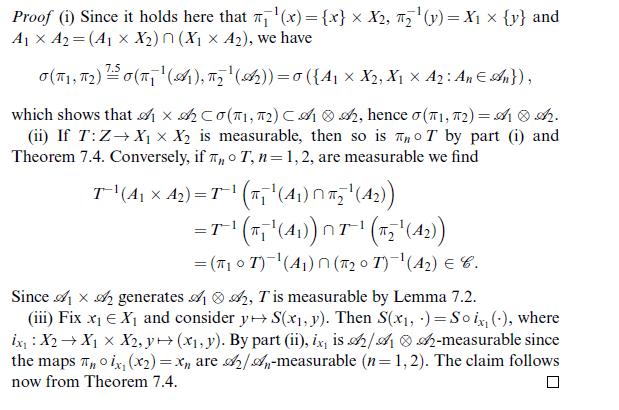
Theorem 14.17 Let (Xn, An), n=1, 2, and (Z, 6) be measurable spaces.