Let u , w 0 u , w 0 be measurable functions on a -finite measure space ( X , A

Let $u,w⩾0$ be measurable functions on a $\sigma$-finite measure space $(X,A,\mu )$.

(i) Show that $t\mu \{u⩾t\}⩽{\int }_{\{u⩾t\}}wd\mu$ for all $t>0$ implies that

$$\int u^{p}d\mu ⩽\frac{p}{p-1}\int u^{p-1}wd\mu \forall p>1$$

(ii) Assume that $u,w\in L^p$. Conclude from (i) that $\parallel u{\parallel }_p⩽\left(p/\right(p-1\left)\right)\parallel w{\parallel }_p$ for $p>1$.

[use the technique of the proof of Theorem 25.12 ; for (ii) use Hölder's inequality.]

Data from theorem 25.12 

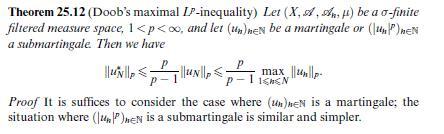
Theorem 25.12 (Doob's maximal IP-inequality) Let (X, A., H) be a o-finite filtered measure space, 1