Let \((X, \mathscr{A}, \mu)\) be a general measure space and let \(u \in \bigcap_{p \geqslant 1} \mathcal{L}^{p}(\mu)\). Then

\[\lim _{p ightarrow \infty}\|u\|_{p}=\|u\|_{\infty}\]

where \(\|u\|_{\infty}=\infty\) if \(u\) is unbounded.

[start with \(\|u\|_{\infty}(1-\epsilon)\|u\|_{\infty}ight\}ight)^{1 / p}(1-\epsilon)\|u\|_{\infty}\) and \(p ightarrow \infty, \epsilon ightarrow 0\), see also the hint to Problem 13.20 , where \(\mu(\ldots)\) is finite in view of the Markov inequality. If \(\|u\|_{\infty}=\infty\), use the First part of the hint and observe that

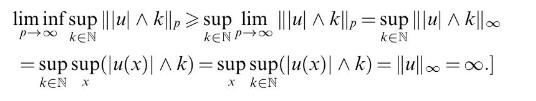
Data from problem 13.20

Let \((X, \mathscr{A}, \mu)\) be a finite measure space and \(u \in \mathcal{M}(\mathscr{A})\) be a bounded function with \(\|u\|_{\infty}>0\). Prove that for all \(n \in \mathbb{N}\)
(i) \(M_{n}:=\int|u|^{n} d \mu \in(0, \infty)\);
(ii) \(M_{n+1} M_{n-1} \geqslant M_{n}^{2}\);
(iii) \(\mu(X)^{-1 / n}\|u\|_{n} \leqslant M_{n+1} / M_{n} \leqslant\|u\|_{\infty}\);
(iv) \(\lim _{n ightarrow \infty} M_{n+1} / M_{n}=\|u\|_{\infty}\).
[for (ii) use Hölder's inequality; for (iii) use Jensen's inequality for the lower estimate and use Hölder's inequality for the upper estimate; and for (iv) observe that \(\int u^{n} d \mu \geqslant \int_{\left\{u>\|u\|_{\infty}-\epsilonight\}}\left(\|u\|_{\infty}-\epsilonight)^{n} d \mu=\mu\left\{u>\|u\|_{\infty}-\epsilonight\}\left(\|u\|_{\infty}-\epsilonight)^{n}\), take the \(n\)th root and let \(n ightarrow \infty\).]

Transcribed Image Text:

lim inf sup |||uk|p>sup lim |||u| k|p=sup |||u| k|| P KEN KENP KEN = sup sup(|u(x)| Ak) = sup sup(|u(x)| Ak) = ||u|| = 0.] KEN X x KEN