Let ((X, mathscr{A}, mu)) be a (sigma)-finite measure space, (f in mathcal{M}(mathscr{A})) and (1 leqslant p (i)
Question:
Let \((X, \mathscr{A}, \mu)\) be a \(\sigma\)-finite measure space, \(f \in \mathcal{M}(\mathscr{A})\) and \(1 \leqslant p
(i) If \(f \in L^{p}(\mu)\), then \(\|f\|_{p}=\sup \left\{\int f g d \mu: g \in L^{q}(\mu),\|g\|_{q} \leqslant 1ight\}\).
(ii) Show that we can replace in (i) the set \(L^{q}(\mu)\) with a dense subset \(\mathcal{D} \subset L^{q}(\mu)\).
(iii) If \(f g \in L^{1}(\mu)\) for all \(g \in L^{q}(\mu)\), then \(f \in L^{p}(\mu)\).
[consider \(g \mapsto I_{f}(g)=\int|f| g d \mu\) and use Theorem 21.5 .]
Data from theorem 21.5
![Theorem 21.5 (Riesz) Let (X,,u) be a o-finite measure space, p = [1,00) and qe (1,00] conjugate indices.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/9/1/3/97265ae2e74285a01705913971457.jpg)

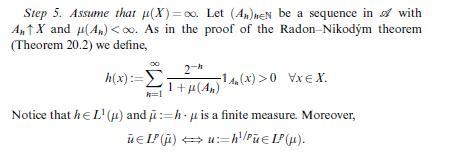

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





