FREE Trial

State and prove Theorem 28.6 and Corollary 28.8 for an arbitrary compact interval ([a, b]). Data from

Question:

State and prove Theorem 28.6 and Corollary 28.8 for an arbitrary compact interval \([a, b]\).

Data from theorem 28.6

Theorem 28.6 (Weierstra) Polynomials are dense in C[0, 1] w.r.t. uniform convergence. Proof (S. N. Bernstein)

since the function p-p(1-p) attains its maximum at p=1/2. As u C[0, 1] is uniformly continuous, u(x) - u(y) |

Data from corollary  28.8

Corollary 28.8 The monomials (t")neN, are complete in L= L ([0, 1], dt), that is, 0,11u(t)t" dt=0 for all

By Weierstra' approximation theorem there is a sequence of polynomials (Pn)neN which approximate u uniformly

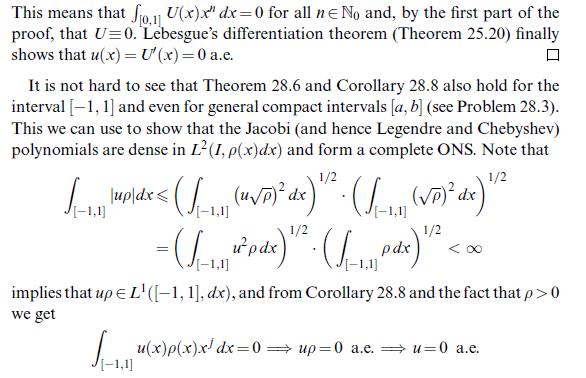
This means that 0.11(x)x" dx=0 for all ne No and, by the first part of the proof, that U=0. Lebesgue'sThis does not quite work for the Hermite and Laguerre polynomials, which are defined on infinite intervals.

The Trigonometric System and Fourier Series We consider now L = L((-, ), B(-, ), =|(-)). As before we use dx

(28.2) follows easily from the classical result that for j, k = No and l, mN 0, if kj, I cos(jx) cos(kx) dx =

Transcribed Image Text:

Theorem 28.6 (Weierstra) Polynomials are dense in C[0, 1] w.r.t. uniform convergence. Proof (S. N. Bernstein) Take sequence (Si)ieN of independent2 measur- able functions on ([0, 1], [0, 1], dx) which are Bernoulli (p, 1 - p)-distributed, 0

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Answer rating: 75% (4 reviews)

Theorem 286 The polynomials are dense in Ca b with respect to uniform convergence ...View the full answer


answer-question-section
Answered By
tutor-profile-image
Khurram shahzad
I am an experienced tutor and have more than 7 years’ experience in the field of tutoring. My areas of expertise are Technology, statistics tasks I also tutor in Social Sciences, Humanities, Marketing, Project Management, Geology, Earth Sciences, Life Sciences, Computer Sciences, Physics, Psychology, Law Engineering, Media Studies, IR and many others. I have been writing blogs, Tech news article, and listicles for American and UK based websites.
4.90+ 5+ Reviews 17+ Question Solved
Related Book For  book-img-for-question
Measures Integrals And Martingales

Measures Integrals And Martingales

ISBN: 9781316620243

2nd Edition

Authors: René L. Schilling

See More Books
Question Posted:
See More Questions

Students also viewed these Business questions

Special Edition Using Microsoft Windows 2000 Professional 1st Edition - ISBN: 9780789721259 - Free Book