Young functions. Let \(\phi:[0, \infty) ightarrow[0, \infty)\) be a strictly increasing continuous function such that \(\phi(0)=0\) and \(\lim _{\xi ightarrow \infty} \phi(\xi)=\infty\). Denote by \(\psi(\eta):=\phi^{-1}(\eta)\) the inverse function. The functions

\[\Phi(A):=\int_{[0, A)} \phi(\xi) \lambda^{1}(d \xi) \quad \text { and } \quad \Psi(B):=\int_{[0, B)} \psi(\eta) \lambda^{1}(d \eta)\]

are called conjugate Young functions. Adapt the proof of Lemma 13.1 to show the following general Young inequality:

\[A B \leqslant \Phi(A)+\Psi(B) \quad \forall A, B \geqslant 0 .\]

[ interpret \(\Phi(A)\) and \(\Psi(B)\) as areas below the graph of \(\phi(\xi)\) resp. \(\psi(\eta)\).]

Data from lemma 13.1

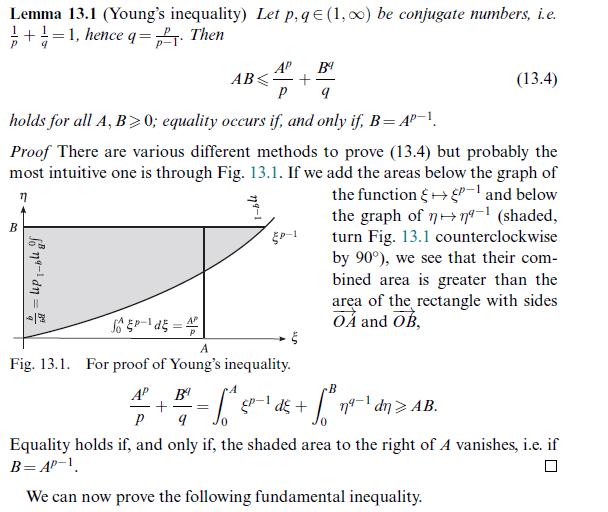
Lemma 13.1 (Young's inequality) Let p, qe (1,00) be conjugate numbers, i.e. 1+1=1, hence q=1. Then B fon-1dn = P 9 holds for all A, B>0; equality occurs if, and only if, B = AP-1 Proof There are various different methods to prove (13.4) but probably the most intuitive one is through Fig. 13.1. If we add the areas below the graph of the function - and below the graph of n (shaded, turn Fig. 13.1 counterclockwise by 90), we see that their com- bined area is greater than the area of the rectangle with sides OA and OB, SEP- dE= AP AB < + AP 5P-1 A Fig. 13.1. For proof of Young's inequality. 7=6 B 5. EP de + AP B + P Equality holds if, and only if, the shaded area to the right of A vanishes, i.e. if B=AP-1 We can now prove the following fundamental inequality. (13.4) nu-1 dn > AB.