A machine tool is mounted on two nonlinear elastic mounts, as shown in Fig. 13.36. The equations of motion, in terms of the coordinates \(x(t)\) and \(\theta(t)\), are given by

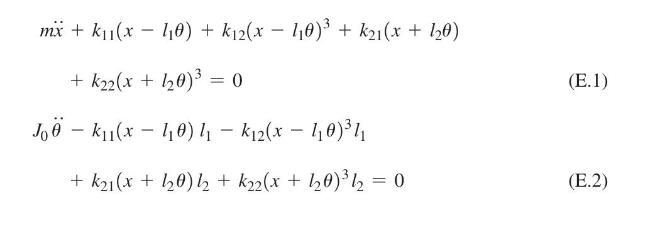
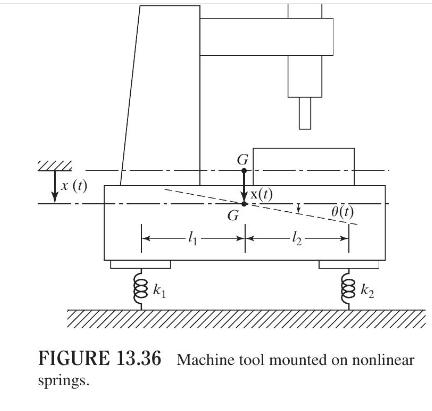
where \(m\) is the mass and \(J_{0}\) is the mass moment of inertia about \(G\) of the machine tool. Using the Runge-Kutta method, find \(x(t)\) and \(\theta(t)\) for the following data: \(m=1000 \mathrm{~kg}\), \(J_{0}=2500 \mathrm{~kg}-\mathrm{m}^{2}, l_{1}=1 \mathrm{~m}, l_{2}=1.5 \mathrm{~m}, k_{1}=40 x_{1}+10 x_{1}^{3} \mathrm{kN} / \mathrm{m}, \quad\) and \(\quad k_{2}=50 x_{2}+\) \(5 x_{2}^{3} \mathrm{kN} / \mathrm{m}\).

mx + k(x - 10) + k12(x 110) + k21(x + 120) + K22(x + 120) = 0 - - J k(x 10) 4 - 12(x - 10) 11 +k21(x+120) 2+ k22(x + 120) = 0 (E.1) (E.2)