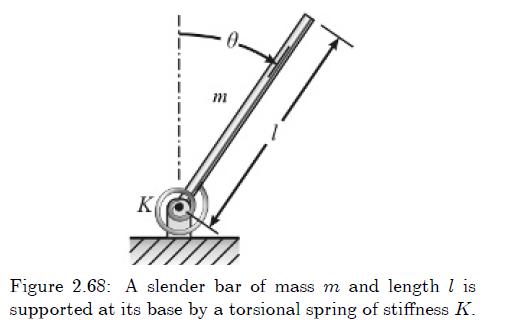
A slender bar of mass \(m\) and length \(l\) is supported at its base by a torsional spring of stiffness \(K\), as per Figure 2.68. The bar rests in the vertical position when in equilibrium with the spring unstretched. Show that the differential equation of rotation \(\theta\) from equilibrium is

\[ \frac{m l^{2}}{3} \ddot{\theta}+K \theta-\frac{m g l}{2} \sin \theta=0 \]

For small vibration, that is, \(\theta \ll 1\), show that the natural frequency is given by

\[ \omega_{n}=\frac{(K-m g l / 2)}{m l^{2} / 3} \]

Transcribed Image Text:

K m Figure 2.68: A slender bar of mass m and length 1 is supported at its base by a torsional spring of stiffness K.