Show that the convolution integral, Eq. (4.31), can also be expressed in terms of the response to

Question:

Show that the convolution integral, Eq. (4.31), can also be expressed in terms of the response to a unit step function $h(t)$ as

\[x(t)=F(0) h(t)+\int_{0}^{t} \frac{d F(\tau)}{d \tau} h(t-\tau) d \tau\]

Equation 4.31:-

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Mechanical Vibrations

ISBN: 9780134361925

6th Edition

Authors: Singiresu S Rao

See More Books

Question Posted: Apr 30, 2024 07:58 AM

See More Questions

Write a paper in which you: 1. Describe the reasons for Disneys adoption of ITIL. 2. Examine the results that were attained by Disney. 3. Compare and contrast ITIL, Committee of Sponsoring...
QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...
(i) Write down the linear program relaxation for the vertex cover problem and solve the linear program. [6 marks] (ii) Based on the solution of the linear program in (b)(i), derive an integer...
Montage Pty Limited (Montage) is a resident private company and is not a base rate entity. Which of the following transactions would result in a debit entry to Montage's franking account? Payment of...
Vickie Plato, accounting clerk in the personnel office of Streisand Corp., has begun to compute pension expense for 2016 but is not sure whether or not she should include the amortization of...
The information that follows relates to equipment owned by Gaurav Limited at December 31, 2017: Cost ...................................................................................... $10,000,000...
You are a CPA engaged in an examination of the financial statements of Pate Corporation for the year ended December 31, 19X3. The financial statements and records of Pate Corporation have not been...
If you anticipate that the price of a stock will rise, you could (1) buy the stock, (2) buy a call, (3) sell a covered call, or (4) sell a put. All four positions may generate profits if the price of...
WRT, a calendar year S corporation, has 100 shares of outstanding stock. At the beginning of the year, Mr. Wallace owned all 100 shares. On September 30, he gave 25 shares to his brother and 40...
Find the response of the rigid bar shown in Fig. 4.53 using convolution integral for the following data: \(k_{1}=k_{2}=5000 \mathrm{~N} / \mathrm{m}, a=0.25 \mathrm{~m}, b=0.5 \mathrm{~m}, l=1.0...
Show that the response to a unit step function $h(t)\left(F_{0}=1 ight.$ in Fig. 4.10(b)) is related to the impulse response function $g(t)$, Eq. (4.25), as follows: \[g(t)=\frac{d h(t)}{d t}\]...
You are studying with some classmates, and you are reviewing each others responses to the following question: If a company failed to reclassify the current portion of its long-term debt, what...
The gecko in the photo is sticking upside down to a smooth ceiling. The remarkable adhesion might be due to static electricity. Gecko feet are covered with microscopic hairs. When these hairs rub...
This scanning electron microscope image of a bacterium was produced using a beam of electrons accelerated through an 30 kV potential difference. What is the speed of the electrons?
Omega, Inc., controls 80 percent of the market for telecommunications equipment in the southeastern United States. To show that Omega is monopolizing that market in violation of the Sherman Act...
When you want to turn a bicycle left, the first thing you do is lean left. Why is it important to do this?
The amounts of time that 5000 randomly selected individual taxpayers used to prepare their federal tax returns. Answer the following questions: a. How many modes would you expect for the...
What are the different mechanisms for transferring energy to or from a control volume? Discuss.
Modify the counter from Exercise 5.44 such that the counter will either increment by 4 or load a new 32-bit value, D, on each clock edge, depending on a control signal Load. When Load = 1, the...
What change management model (such as Lewin's, Kotter's, or ADKAR) should be used, and why? What are the set of steps used in the model you chose? What can the CEO' do to address resistance to change...
1. Solve the following inequalities: 304(2x-3) 200 2. 3. 1 1 2 3 < 5 - 6
The functions f and g are defined as follows. f(x)=-5x+2 g(x)=-4x-3 Find f (6) and g (5). Simplify your answers as much as possible.

Show that the convolution integral, Eq. (4.31), can also be expressed in terms of the response to

Question:

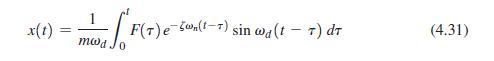
F(T)e (-) sin wd (t - T) dr (4.31) x(t) == mwd F(T

Step by Step Answer:

Mechanical Vibrations

Students also viewed these Engineering questions