A torus can be defined by two radii: A large radius \(R\) running around the center of the torus, and a small radius \(r\) corresponding to a cross-sectional slice. Let \(R\) live in the \(x, y\) plane. Then if \(\varphi\) is an angle relative to the \(x\) axis and lying in the \(x, y\) plane, and \(\theta\) is an angle within a cross-sectional slice, with \(\theta=0\) corresponding to the outermost radius of the torus \(R+r\), then the Cartesian coordinates of points on the torus are

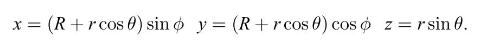
x= (R+rcos) sino y = (R+rcos 0) cos z = r sin 0.