Classical big-bang cosmological models. Consider a very large sphere of uniform-density dust of mass density \(ho(t)\). That is, at any given time the density is the same everywhere within the sphere, but the density decreases with time if the sphere expands, or increases with time if the sphere contracts, so that the total mass of the sphere remains fixed. At time \(t=0\) the sphere is all gathered at the origin, with infinite density and infinite outward velocity, so it is undergoing a "big bang" explosion. At some instant \(t_{0}\) after the big bang the density everywhere within the sphere is \(ho_{0}\) and the outward speed of a particular dust particle at radius \(r_{0}\) is \(v_{0}\). Use Newton's gravitational constant \(G\) and also the result found in problem 1.41, that in spherical symmetry only those mass-shells whose radius \(r\) is less than the radius of the particular dust particle exert a net force on the particle. Let \(M_{r}\) be the (time-independent) total mass within radius \(r\).

(a) Find an expression for \(r(t)\), the radius of the particle as a function of time, supposing that the particle has the escape velocity. That is, the particle, in common with all particles in the sphere, keeps moving outward but slows down, approaching zero velocity as \(r ightarrow \infty\).

(b) Then consider the same model of spherically-symmetric dust, except that instead of having the escape velocity, each dust particle has at any moment a velocity less than the escape velocity for that particle. This means that the energy of a particle of mass \(m\) is negative, where

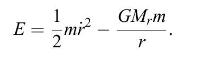
and where \(r(t)\) is its distance from the center of the sphere. Show that in this case the time \(t(r)\) expressed in terms of \(r\) can be written

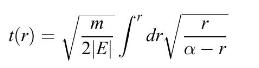
and find the constant \(\alpha\) in terms of \(G, M_{r}, m\), and \(|E|\).

(c) To perform the integration, substitute \(r=\alpha \sin ^{2}(\eta / 2) \equiv(\alpha / 2)(1-\cos \eta)\), where \(\eta\) is a new variable, and show that

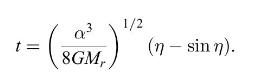
(d) Make a table of \(t\) and \(r\) for a few values of \(\eta\) between 0 and \(2 \pi\), and plot \(r(t)\) for these values. The resulting shape is a cycloid, and the equations for \(t(\eta)\) and \(r(\eta)\) are in fact the parametric equations for a cycloid. Note that this negative-energy cosmological model begins with a "big bang" and ends with a "big crunch."

(e) Finally, consider the same model of spherically-symmetric dust, except that instead of having the escape velocity or less, dust particles have at any moment a velocity greater than the escape velocity. This means that the energy of a dust particle of mass \(m\) is positive. Using an approach analogous to that just used for negative-energy cosmologies, show that in this case

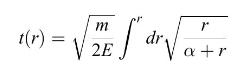
and find the constant \(\alpha\) in terms of \(G, M_{r}, m\), and \(E\).

(f) Perform the integration by substituting \(r=\alpha \sinh ^{2}(\eta / 2) \equiv(\alpha / 2)(\cosh \eta-1)\), where \(\eta\) is a new variable and sinh and cosh are hyperbolic sine and hyperbolic cosine functions, respectively. (g) Then

write the solution in parametric form, analogous to that just carried out for negative-energy cosmologies. That is, give formulas for both \(t(\eta)\) and \(r(\eta)\) for positive-energy cosmologies. (h) Make a table of \(t\) and \(r\) for several values of \(\eta\), and plot \(r(t)\) for these values. What is the ultimate fate of such a classical model universe?

Transcribed Image Text:

E= 1 mi2 GM,m r