Example 4.2 featured a bead sliding on a vertically-oriented helix of radius \(R\). The angle \(\theta\) about the symmetry axis was related to its vertical coordinate \(z\) on the wire by \(\theta=\alpha z\). There is a uniform gravitational field \(g\) vertically downward.

(a) Rewrite the Lagrangian and find the Lagrange equation, using \(\theta\) as the generalized coordinate.

(b) Are there any conserved dynamical quantities?

(c) Write the simplest differential equation of motion of the bead, and go as far as you can to solve analytically for \(\theta\) as a function of time.

Data from Example 4.2

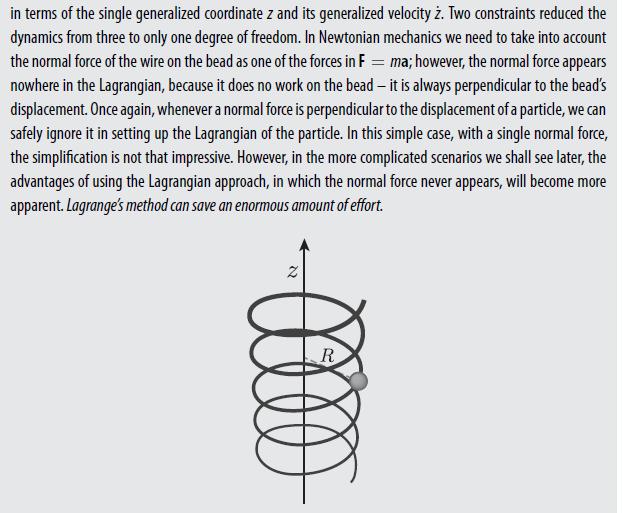
A bead sliding on a vertically oriented helical wire.

A bead of mass m is slipped onto a frictionless wire wound in the shape of a helix of radius R, whose symmetry axis is oriented vertically in a uniform gravitational field, as shown in Figure 4.3. As always, we assume the description is from an inertial frame's perspective (unless explicitly stated otherwise). Using cylindrical coordinates p, 4,z, the base of the helix is located atz = 0, = 0, and the angle is related to the height zat any point by =az, where a is a constant with dimensions of inverse length. The gravitational potential energy of the bead is U = mgz, and its kinetic energy is T = (1/2)mv = (1/2)m[p + px + ]. However, the bead is constrained to move along the helix, so the bead's radius is constant at p = R, and (choosing z as the single generalized coordinate), = az. Therefore the kinetic energy of the bead is T 1 1 1 = m v = m (x + y + ) == m (p + 1 +2) = (1/2)m[0+ aR + 1], (4.11) where we switched to cylindrical coordinates first and then implemented the two constraints = az and p = R. So the Lagrangian of the bead is 1 L = T - U = m[1 + a R] mgz (4.12)