The Friedmann equations have played an important role in relativistic bigbang cosmologies. They feature a scale factor
Question:
The Friedmann equations have played an important role in relativistic bigbang cosmologies. They feature a "scale factor" \(a(t)\), proportional to the distance between any two points (such as the positions of two galaxies) that are sufficiently remote from one another that local random motions can be ignored. If \(a\) increases with time, the distance between galaxies increases proportionally, corresponding to an expanding universe. If we model for simplicity the universe as filled with pressure-free dust of uniform density \(ho\), the Friedmann equations for \(a(t)\) are
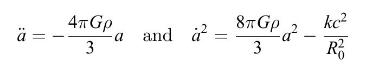
where \(G\) is Newton's gravitational constant, \(c\) is the speed of light, \(R_{0}\) is the distance between two dust particles at some particular time \(t_{0}\), and \(k=+1,-1\), or 0 . The density of the dust is inversely proportional to the cube of the scale factor \(a(t)\), i.e., \(ho=ho_{0}\left(a_{0} / a\right)^{3}\), where \(ho_{0}\) is the density when \(a=a_{0}\). Therefore
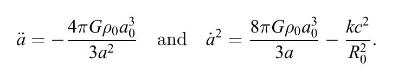
(a) Show that if we set the origin to be at one of the two chosen dust particles, then if \(M\) is the total mass of dust within a sphere surrounding this origin out to the radius of the other chosen particle, and if at arbitrary time \(t_{0}\) we set \(a_{0}=1\), then the equations can be written
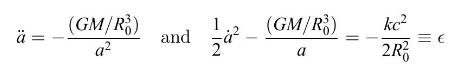
where \(\epsilon\) and \(M\) are constants.
(b) Show that the second equation is a first integral of the first equation.
(c) Compare these equations to the \(F=m a\) and energy conservation equations of a particle moving radially under the influence of the gravity of a spherical moon of mass \(M\).
(d) Einstein hoped that his general-relativistic equations would lead to a static solution for the universe, since he (like just about everyone before him) believed that the universe was basically at rest. The Friedmann equations resulting from his theory show that the universe is generally expanding or contracting, however, just as a rock far from the Earth is not going to stay there, but will generally be either falling inward or on its way out. So Einstein modified his theory with the addition of a "cosmological constant" \(\Lambda\), which changed the Friedmann equations for pressure-free dust to
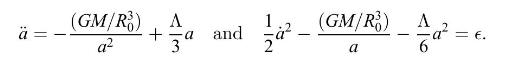
Show that these equations \(d o\) have a static solution, and find the value of \(\Lambda\) for which the solution is static.
(e) Show however (by sketching the effective potential energy function in the second equation) that the static solution is unstable, so that if the universe is kicked even slightly outward it will accelerate outward, or if it is kicked even slightly inward it will collapse. A static solution is therefore physically unrealistic. (Einstein failed to realize that his static solution was unstable, and later, when Edwin Hubble showed from his observations at the Mount Wilson Observatory that the universe is in fact expanding, Einstein declared that introducing the cosmological constant was "my biggest blunder".)
(f) Suppose the cosmological constant is retained in the equations, but that the dust is removed so that \(M=0\). Solve the equations for \(a(t)\) in this case. The solution is the de Sitter model, an "inflationary" model of the expanding universe. What is the constant \(\epsilon\) for the de Sitter model? (g) Make a qualitative sketch of \(a(t)\) if both \(M\) and \(\Lambda\) are positive constants. Of the terms containing \(M\) and \(\Lambda\), which dominates for small times? For large times?
Step by Step Answer:






