Select a $50\mathrm{\%}$ random subsample of the Section 4.6.4 data on log health expenditure $(y)$ and log total expenditure $(x)$.

(a) Obtain OLS estimates and contrast usual and White standard errors for the slope coefficient.

(b) Obtain median regression estimates and compare these to the OLS estimates.

(c) Obtain quantile regression estimates for $q=0.25$ and $q=0.75$.

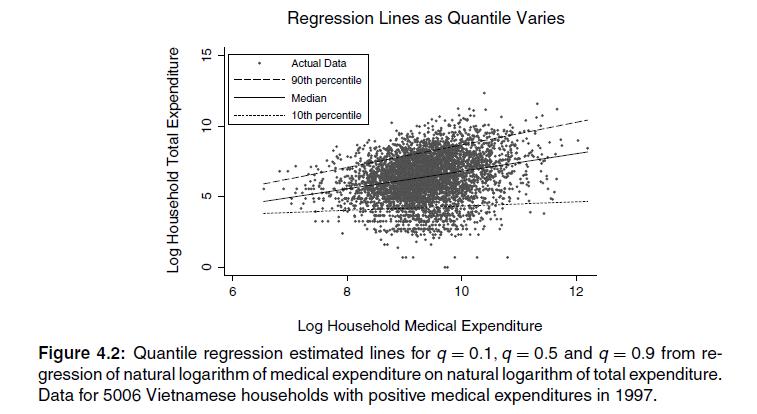
(d) Reproduce Figure 4.2 using your answers from parts (a)-(c).

4.9.4. Finite-Sample Bias This section summarizes a relatively challenging and as yet unfinished literature on "weak instruments" that focuses on the practical problem that even in "large" samples asymptotic theory can provide a poor approximation to the distribution of the IV esti- mator. In particular the IV estimator is biased in finite samples even if asymptotically consistent. The bias can be especially pronounced when instruments are weak. This bias of IV, which is toward the inconsistent OLS estimator, can be remark- ably large, as demonstrated in a simple Monte Carlo experiment by Nelson and Startz (1990), and by a real data application involving several hundred thousand observations but very weak instruments by Bound et al. (1995). Moreover, the standard errors can also be very biased, as also demonstrated by Nelson and Startz (1990). The theoretical literature entails quite specialized and advanced econometric theory, as it is actually difficult to obtain the sample mean of the IV estimator. To see this, consider adapting to the IV estimator the usual proof of unbiasedness of the OLS estimator given in Section 4.4.8. For By defined in (4.51) for the just-identified case this yields E[iv]=+Ez.x,u[(Z'X)-Z'u] =+Ez.x [(Z'X)'Z' [E[u]Z, X]],