(a) Calculate the 1-dimensional Fourier transforms [Eq. (8.11a) reduced to 1 dimension] of the functions f 1 (x) e x2/2 2 , and f

(a) Calculate the 1-dimensional Fourier transforms [Eq. (8.11a) reduced to 1 dimension] of the functions f₁(x) ≡ e^−x2/2σ2, and f₂ ≡ 0 for x 2 ≡ e^−x/h for x ≥ 0.

(b) Take the inverse transforms of your answers to part (a) and recover the original functions.

(c) Convolve the exponential function f₂ with the Gaussian function f₁, and then compute the Fourier transform of their convolution. Verify that the result is the same as the product of the Fourier transforms of f₁ and f₂.

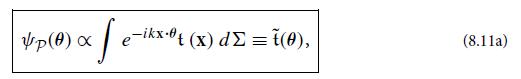
1 x Se = f e-ikx0 + (x) d = i(0), Up(0) x (8.11a).