(a) If y is a random process with spectral density S_y(f), and w(t) is the output of the finite-Fourier-transform filter (6.58a), what is S_w(f)?

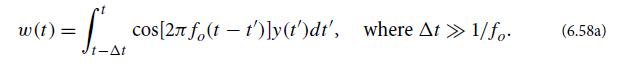
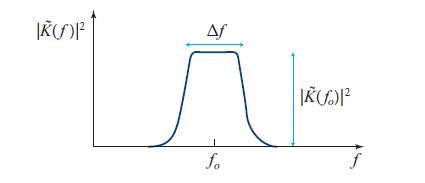
(b) Sketch the filter function |K̃(f)² for this finite-Fourier-transform filter, and show that its bandwidth is given by Eq. (6.58b).

(c) An “averaging filter” is one that averages its input over some fixed time interval △t:

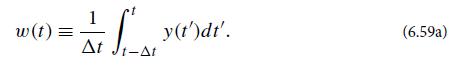
What is |K̃(f)|² for this filter? Draw a sketch of this |K̃(f)|².

(d) Suppose that y(t) has a spectral density that is very nearly constant at all frequencies

and that this y is put through the averaging filter (6.59a). Show that the rms fluctuations in the averaged output w(t) are

where △f, interpretable as the bandwidth of the averaging filter, is

(Recall that in our formalism we insist that f be nonnegative.) Why is there a factor 1/2 here and not one in the equation for an averaging filter [Eq. (6.58b)]? Because here, with f restricted to positive frequencies and the filter centered on zero frequency, we see only the right half of the filter: f ≥ f_o = 0 in Fig. 6.13.

Equation 6.58(b)

Fig. 6.13.

w (t) = L cos[2 fo(t t')ly(t)dt', where At >> 1/fo. (6.58a)