(a) Let a and b be scalar fields with arbitrary but smooth dependence on location in curved spacetime, and let A(vector) and B(vector) be vector fields. Show that

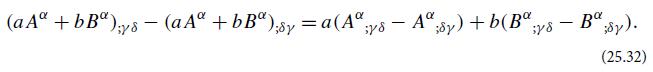
(b) Use Eq. (25.32) to show that 

(i) The commutator of the double gradient is independent of how the differentiated vector field varies from point to point and depends only on the value of the field at the location where the commutator is evaluated.

(ii) The commutator is linear in that value. Thereby conclude that there must exist a fourth-rank tensor field R such that Eq. (25.30) is true for any vector field p(vector).

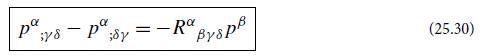
(aAa +bB);ys - (aA + bB");sy = a(A ;) sys - Au;8y) + b(Bays-Ba idy). (25.32)