(a) Show that, if n j is a 3-dimensional unit vector and and are defined as in Eq. (2.37b), then the following is

(a) Show that, if n^j is a 3-dimensional unit vector and β and γ are defined as in Eq. (2.37b), then the following is a Lorentz transformation [i.e., it satisfies Eq. (2.35b)]:

Show, further, that this transformation is a pure boost along the direction n with speed β, and show that the inverse matrix L^μ̅_α for this boost is the same as L^α_μ̅, but with β changed to −β.

(b) Show that the following is also a Lorentz transformation:

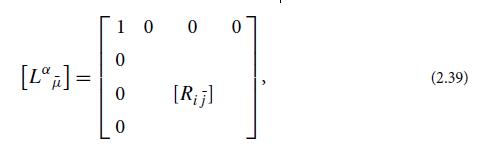
where [R_ij̅] is a 3-dimensional rotation matrix for Euclidean 3-space. Show, further, that this Lorentz transformation rotates the inertial frame’s spatial axes (its latticework of measuring rods) while leaving the frame’s velocity unchanged (i.e., the new frame is at rest with respect to the old).

One can show (not surprisingly) that the general Lorentz transformation [i.e., the general solution of Eqs. (2.35b)] can be expressed as a sequence of pure boosts, pure rotations, and pure inversions (in which one or more of the coordinate axes are reflected through the origin, so x^α =−x_α̅).

L=y, Lj=L=Byn, L= L* j = (y 1)nn* +8jk. (2.38) 3